题目内容
12.已知函数y=f(x)对任意实数x、y∈R满足:f(x•y)=f(x)+f(y)+1.①求f(1)、f(-1)的值;
②证明:函数y=f(x)在R上是偶函数.
分析 ①通过x=y=1,即可求解f(1)的值,通过令x=y=-1,即可求解f(-1)的值.
②令x=-1,用-x换y,化简方程,即可证明函数是偶函数.
解答 解:①函数y=f(x)对任意实数x、y∈R满足:f(x•y)=f(x)+f(y)+1,
令x=y=1,可得:f(1)=f(1)+f(1)+1,可得f(1)=-1,
令x=y=-1可得:f(1)=f(-1)+f(-1)+1,
解得f(-1)=-1.
②证明:令x=-1,-x换y,可得f(x)=f(-1)+f(-x)+1=f(-x),
即f(-x)=f(x).
函数y=f(x)在R上是偶函数.
点评 本题考查抽象函数的应用,赋值法的应用,考查转化思想以及计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.已知△ABC的内角A,B,C的对边分别为a,b,c,设$\overrightarrow{p}$=(c-b,c-a),$\overrightarrow{q}$=(sinA,sinB+sinC),且$\overrightarrow{p}$∥$\overrightarrow{q}$,则B=( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{3π}{4}$ |
17.等差数列{an}的前n项和为Sn,若S25>0,S26<0,则Sn最大时n=( )
| A. | 12 | B. | 13 | C. | 15 | D. | 25 |
4. 已知实数x,y的取值如表所示.
已知实数x,y的取值如表所示.
(1)请根据上表数据在网格纸中绘制散点图;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$.
注:回归方程为$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$,其中$\widehat{b}$=$\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2}-n{{(\overline x)}^2}}}$,a=$\overline y-b\overline x$.
 已知实数x,y的取值如表所示.
已知实数x,y的取值如表所示.| x | 0 | 1 | 2 | 3 | 4 |
| y | 1 | 2 | 4 | 6 | 5 |
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$.
注:回归方程为$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$,其中$\widehat{b}$=$\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2}-n{{(\overline x)}^2}}}$,a=$\overline y-b\overline x$.
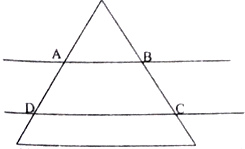 将边长为4正三角形薄片,用平行于底边的两条直线剪成三块(如图所示),这两条平行线间的距离为$\sqrt{3}$,其中间一块是梯形记为ABCD,记$S=\frac{{{{({梯形ABCD的周长})}^2}}}{梯形ABCD的面积}$,则S的最小值为$\frac{32\sqrt{3}}{3}$.
将边长为4正三角形薄片,用平行于底边的两条直线剪成三块(如图所示),这两条平行线间的距离为$\sqrt{3}$,其中间一块是梯形记为ABCD,记$S=\frac{{{{({梯形ABCD的周长})}^2}}}{梯形ABCD的面积}$,则S的最小值为$\frac{32\sqrt{3}}{3}$.