题目内容
17.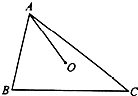 如图,在△ABC中,AB=5,AC=9,若O为△ABC内一点,且满足|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=|$\overrightarrow{OC}$|,则$\overrightarrow{AO}$•$\overrightarrow{BC}$的值是28.
如图,在△ABC中,AB=5,AC=9,若O为△ABC内一点,且满足|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=|$\overrightarrow{OC}$|,则$\overrightarrow{AO}$•$\overrightarrow{BC}$的值是28.
分析 如图所示,取BC的中点D,连接OD,AD.则$\overrightarrow{AD}$=$\frac{1}{2}$($\overrightarrow{AB}$+$\overrightarrow{AC}$),OD⊥BC,即$\overrightarrow{OD}$•$\overrightarrow{BC}$=0.于是$\overrightarrow{AO}$•$\overrightarrow{BC}$=($\overrightarrow{AD}$+$\overrightarrow{DO}$)•$\overrightarrow{BC}$=$\overrightarrow{AD}$•$\overrightarrow{BC}$+$\overrightarrow{DO}$•$\overrightarrow{BC}$=$\overrightarrow{AD}$•$\overrightarrow{BC}$=$\frac{1}{2}$($\overrightarrow{AB}$+$\overrightarrow{AC}$)•($\overrightarrow{AC}$-$\overrightarrow{AB}$),化简代入即可得出.
解答 解:由题意,|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=|$\overrightarrow{OC}$|,则O是外心.
如图所示,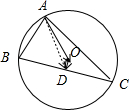 取BC的中点D,连接OD,AD.
取BC的中点D,连接OD,AD.
则$\overrightarrow{AD}$=$\frac{1}{2}$($\overrightarrow{AB}$+$\overrightarrow{AC}$),OD⊥BC,即$\overrightarrow{OD}$•$\overrightarrow{BC}$=0.
∴$\overrightarrow{AO}$•$\overrightarrow{BC}$=($\overrightarrow{AD}$+$\overrightarrow{DO}$)•$\overrightarrow{BC}$=$\overrightarrow{AD}$•$\overrightarrow{BC}$+$\overrightarrow{DO}$•$\overrightarrow{BC}$=$\overrightarrow{AD}$•$\overrightarrow{BC}$
=$\frac{1}{2}$($\overrightarrow{AB}$+$\overrightarrow{AC}$)•($\overrightarrow{AC}$-$\overrightarrow{AB}$)
=$\frac{1}{2}$($\overrightarrow{AC}$2-$\overrightarrow{AB}$2)=$\frac{1}{2}$(81-25)=28.
故答案为:28.
点评 本题考查了数量积运算性质、向量平行四边形法则、垂经定理、向量垂直与数量积的关系,考查了推理能力与计算能力,属于中档题.

 名校课堂系列答案
名校课堂系列答案| A. | [0,1] | B. | (0,1] | C. | (0,1) | D. | (-1,0) |
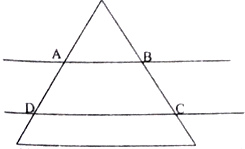 将边长为4正三角形薄片,用平行于底边的两条直线剪成三块(如图所示),这两条平行线间的距离为$\sqrt{3}$,其中间一块是梯形记为ABCD,记$S=\frac{{{{({梯形ABCD的周长})}^2}}}{梯形ABCD的面积}$,则S的最小值为$\frac{32\sqrt{3}}{3}$.
将边长为4正三角形薄片,用平行于底边的两条直线剪成三块(如图所示),这两条平行线间的距离为$\sqrt{3}$,其中间一块是梯形记为ABCD,记$S=\frac{{{{({梯形ABCD的周长})}^2}}}{梯形ABCD的面积}$,则S的最小值为$\frac{32\sqrt{3}}{3}$.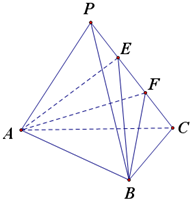 在三棱锥P-ABC中,PA=PB=PC=3,AB=$\sqrt{6}$,BC=$\sqrt{3}$,AB⊥BC,E,F为PC的三等分点.
在三棱锥P-ABC中,PA=PB=PC=3,AB=$\sqrt{6}$,BC=$\sqrt{3}$,AB⊥BC,E,F为PC的三等分点.