题目内容
15.某公司在一次对员工的休闲方式(看电视与运动)与性别之间是否有关系的调查中,共调查了124人,其中女性70人中主要休闲方式是看电视的有43人,男性中主要休闲方式是运动的有33人.(1)根据以上数据建立一个2×2的列联表;
(2)检验性别与休闲方式是否有关系.
${Χ^2}=\frac{{n{{({n_{11}}{n_{22}}-{n_{12}}{n_{21}})}^2}}}{{{n_{1+}}{n_{2+}}{n_{+1}}{n_{+2}}}}$
| P(Χ2≥k) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
分析 (1)利用已知条件写出联列表即可.
(2)利用公式求出χ2,然后推出检验性别与休闲方式是否有关系.
解答 解:(1)2×2的列联表:
| 休闲方式 性别 | 看电视 | 运动 | 合计 |
| 女 | 43 | 27 | 70 |
| 男 | 21 | 33 | 54 |
| 合计. | 64 | 60 | 124 |
χ2=$\frac{124×(43×33-27×21)2}{70×54×64×60}$≈6.201.
因为χ2>5.024,所以有97.5%的把握认为休闲方式与性别有关系.
点评 本题考查独立检验的应用,考查计算能力.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
6.5个人分4张无座足球票,每人至多分一张,而且必须分完,不同的分发种数有( )
| A. | $A_5^4$种 | B. | 45种 | C. | $C_5^4$种 | D. | 54种 |
20.已知△ABC的内角A,B,C的对边分别为a,b,c,设$\overrightarrow{p}$=(c-b,c-a),$\overrightarrow{q}$=(sinA,sinB+sinC),且$\overrightarrow{p}$∥$\overrightarrow{q}$,则B=( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{3π}{4}$ |
4.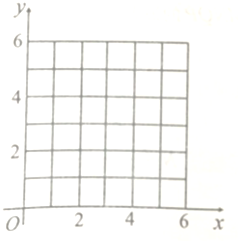 已知实数x,y的取值如表所示.
已知实数x,y的取值如表所示.
(1)请根据上表数据在网格纸中绘制散点图;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$.
注:回归方程为$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$,其中$\widehat{b}$=$\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2}-n{{(\overline x)}^2}}}$,a=$\overline y-b\overline x$.
 已知实数x,y的取值如表所示.
已知实数x,y的取值如表所示.| x | 0 | 1 | 2 | 3 | 4 |
| y | 1 | 2 | 4 | 6 | 5 |
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$.
注:回归方程为$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$,其中$\widehat{b}$=$\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2}-n{{(\overline x)}^2}}}$,a=$\overline y-b\overline x$.
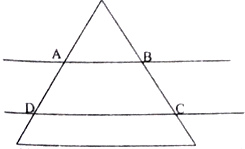 将边长为4正三角形薄片,用平行于底边的两条直线剪成三块(如图所示),这两条平行线间的距离为$\sqrt{3}$,其中间一块是梯形记为ABCD,记$S=\frac{{{{({梯形ABCD的周长})}^2}}}{梯形ABCD的面积}$,则S的最小值为$\frac{32\sqrt{3}}{3}$.
将边长为4正三角形薄片,用平行于底边的两条直线剪成三块(如图所示),这两条平行线间的距离为$\sqrt{3}$,其中间一块是梯形记为ABCD,记$S=\frac{{{{({梯形ABCD的周长})}^2}}}{梯形ABCD的面积}$,则S的最小值为$\frac{32\sqrt{3}}{3}$.