题目内容
19.已知矩阵A=$[\begin{array}{l}{a}&{1}\\{b}&{0}\end{array}]$,其中a,b∈R,若点P(1,1)在矩阵A的变换下得到点Q(3,3),向量$\overrightarrow{β}$=$[\begin{array}{l}{5}\\{9}\end{array}]$.(1)求a,b的值及矩阵A的特征值、特征向量;
(2)计算A20$\overrightarrow{β}$.
分析 (1)根据矩阵的坐标变换,代入,列方程组,即可求得a和b的值,求得矩阵A,求得矩阵A的特征多项式f(λ),令f(λ)=0,求得特征值,根据特征值求得特征向量;
(2)令β=mα1+nα2,代入求得m和n的值,根据矩阵的乘法即可求得A20$\overrightarrow{β}$的值.
解答 解:(1)由题知$[\begin{array}{l}2\;\;a\\ b\;\;0\end{array}][\begin{array}{l}1\\ 1\end{array}]=[\begin{array}{l}3\\ 3\end{array}]$,即$\left\{\begin{array}{l}{2+a=3}\\{b=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=1}\\{b=3}\end{array}\right.$,
所以A=$[\begin{array}{l}{2}&{1}\\{3}&{0}\end{array}]$.…(2分)
矩阵A的特征多项式为f(λ)=$|\begin{array}{l}{λ-2}&{-1}\\{-3}&{λ}\end{array}|$=λ(λ-2)-3=0,
所以λ1=-1,λ2=3,设对应的特征向量为α1=$[\begin{array}{l}{{x}_{1}}\\{{y}_{1}}\end{array}]$,α2=$[\begin{array}{l}{{x}_{2}}\\{{y}_{2}}\end{array}]$.
由Aα1=λ1α1,Aα2=λ2α2,可得3x1+y1=0,x2-y2=0,
故属于特征值λ1=-1的一个特征向量为α1=$[\begin{array}{l}{1}\\{-3}\end{array}]$,
属于特征值λ2=3的一个特征向量为α2=$[\begin{array}{l}{1}\\{1}\end{array}]$.…(8分)
(2)令β=mα1+nα2,则$[\begin{array}{l}{5}\\{9}\end{array}]$=m$[\begin{array}{l}{1}\\{-3}\end{array}]$+n$[\begin{array}{l}{1}\\{1}\end{array}]$,
解得m=-1,n=6. …(10分)
所以${A^{20}}β={A^{20}}(-2{α_1}+3{α_2})=-1×({A^{20}}{α_1})+6×({A^{20}}{α_2})$,
=-1×(${λ}_{1}^{20}{α}_{1}$)+6×(${λ}_{2}^{20}$α2),
=-1×(-1)20×$[\begin{array}{l}{1}\\{-3}\end{array}]$+6×320×$[\begin{array}{l}{1}\\{2}\end{array}]$,
=$[\begin{array}{l}{2×{3}^{21}-1}\\{2×{3}^{21}+3}\end{array}]$.…(14分)
点评 本题考查矩阵的坐标变换,考查矩阵特征和特征向量的求法,矩阵的乘法,考查计算能力,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 已知实数x,y的取值如表所示.
已知实数x,y的取值如表所示.| x | 0 | 1 | 2 | 3 | 4 |
| y | 1 | 2 | 4 | 6 | 5 |
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$.
注:回归方程为$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$,其中$\widehat{b}$=$\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2}-n{{(\overline x)}^2}}}$,a=$\overline y-b\overline x$.
| A. | [0,1] | B. | (0,1] | C. | (0,1) | D. | (-1,0) |
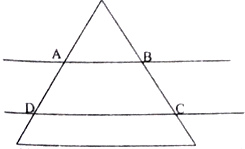 将边长为4正三角形薄片,用平行于底边的两条直线剪成三块(如图所示),这两条平行线间的距离为$\sqrt{3}$,其中间一块是梯形记为ABCD,记$S=\frac{{{{({梯形ABCD的周长})}^2}}}{梯形ABCD的面积}$,则S的最小值为$\frac{32\sqrt{3}}{3}$.
将边长为4正三角形薄片,用平行于底边的两条直线剪成三块(如图所示),这两条平行线间的距离为$\sqrt{3}$,其中间一块是梯形记为ABCD,记$S=\frac{{{{({梯形ABCD的周长})}^2}}}{梯形ABCD的面积}$,则S的最小值为$\frac{32\sqrt{3}}{3}$.