题目内容
20.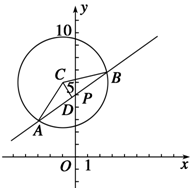 已知圆C过P(2,6),Q(-2,2)两点,且圆心C在直线3x+y=0上.
已知圆C过P(2,6),Q(-2,2)两点,且圆心C在直线3x+y=0上.(1)求圆C的方程.
(2)若直线l过点P(0,5)且被圆C截得的线段长为4$\sqrt{3}$,求l的方程.
分析 (1)把点P、Q的坐标和圆心坐标代入圆的标准方程,利用待定系数法求得系数的值;
(2)分类讨论,斜率存在和斜率不存在两种情况.
①当直线l的斜率不存在时,满足题意,易得直线方程;
②当直线l的斜率存在时,设所求直线l的斜率为k,则直线l的方程为:y-5=kx,由点到直线的距离公式求得k的值.
解答  解:(1)方法一 设圆的方程为x2+y2+Dx+Ey+F=0,依题意有$\left\{\begin{array}{l}{2D+6E+F=0}\\{-2D+2E+F=-8}\\{-\frac{3D}{2}-\frac{E}{2}=0}\end{array}\right.$,
解:(1)方法一 设圆的方程为x2+y2+Dx+Ey+F=0,依题意有$\left\{\begin{array}{l}{2D+6E+F=0}\\{-2D+2E+F=-8}\\{-\frac{3D}{2}-\frac{E}{2}=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{D=4}\\{E=-12}\\{F=24}\end{array}\right.$,
故所求圆的方程为x2+y2+4x-12y+24=0.
(2)如图所示,|AB|=4$\sqrt{3}$,设D是线段AB的中点,
则 CD⊥AB,
∴|AD|=2$\sqrt{3}$,|AC|=4.
在Rt△ACD中,可得|CD|=2.
当直线l的斜率不存在时,满足题意,
此时方程为x=0.
当直线l的斜率存在时,设所求直线l的斜率为k,则直线l的方程为:y-5=kx,
即kx-y+5=0.由点C到直线AB的距离公式:
$\frac{|-2k-6+5|}{\sqrt{k2+1}}$=2,得k=$\frac{3}{4}$,此时直线l的方程为
3x-4y+20=0.
∴所求直线l的方程为x=0或3x-4y+20=0.
点评 本题考查了直线与圆的位置关系,涉及的知识有两点间的距离公式,点到直线的距离公式,圆的标准方程,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.若直线l1:x-2y+1=0与l2:2x+ay-2=0平行,则l1与l2的距离为( )
| A. | $\frac{{\sqrt{5}}}{5}$ | B. | $\frac{{2\sqrt{5}}}{5}$ | C. | $\frac{1}{5}$ | D. | $\frac{2}{5}$ |
15. 某学生为了测试煤气灶烧水如何节省煤气的问题设计了一个实验,并获得了煤气开关旋钮旋转的弧度数x与烧开一壶水所用时间y的一组数据,且作了一定的数据处理(如表),得到了散点图(如图).
某学生为了测试煤气灶烧水如何节省煤气的问题设计了一个实验,并获得了煤气开关旋钮旋转的弧度数x与烧开一壶水所用时间y的一组数据,且作了一定的数据处理(如表),得到了散点图(如图).
表中${w_i}=\frac{1}{x_i^2},\overline{w}=\frac{1}{10}\sum_{i=1}^{10}{w_i}$.
(1)根据散点图判断,y=a+bx与$y=c+\frac{d}{x^2}$哪一个更适宜作烧水时间y关于开关旋钮旋转的弧度数x的回归方程类型?(不必说明理由)
(2)根据判断结果和表中数据,建立y关于x的回归方程;
(3)若旋转的弧度数x与单位时间内煤气输出量t成正比,那么x为多少时,烧开一壶水最省煤气?
附:对于一组数据(u1,v1),(u2,v2),(u3,v3),…,(un,vn),其回归直线v=α+βu的斜率和截距的最小二乘估计分别为$\hat β=\frac{{\sum_{i=1}^n{({v_i}-\bar v)({u_i}-\bar u)}}}{{\sum_{i=1}^n{{{({u_i}-\bar u)}^2}}}},\hat α=\bar v-\hat β\bar u$.
 某学生为了测试煤气灶烧水如何节省煤气的问题设计了一个实验,并获得了煤气开关旋钮旋转的弧度数x与烧开一壶水所用时间y的一组数据,且作了一定的数据处理(如表),得到了散点图(如图).
某学生为了测试煤气灶烧水如何节省煤气的问题设计了一个实验,并获得了煤气开关旋钮旋转的弧度数x与烧开一壶水所用时间y的一组数据,且作了一定的数据处理(如表),得到了散点图(如图).| $\bar x$ | $\bar y$ | $\bar w$ | $\sum_{i=1}^{10}{({x_i}-\bar x)^2}$ | $\sum_{i=1}^{10}{({w_i}-\bar w)^2}$ | $\sum_{i=1}^{10}({x_i}-\bar x)({y_i}-\bar y)$ | $\sum_{i=1}^{10}({w_i}-\bar w)({y_i}-\bar y)$ |
| 1.47 | 20.6 | 0.78 | 2.35 | 0.81 | -19.3 | 16.2 |
(1)根据散点图判断,y=a+bx与$y=c+\frac{d}{x^2}$哪一个更适宜作烧水时间y关于开关旋钮旋转的弧度数x的回归方程类型?(不必说明理由)
(2)根据判断结果和表中数据,建立y关于x的回归方程;
(3)若旋转的弧度数x与单位时间内煤气输出量t成正比,那么x为多少时,烧开一壶水最省煤气?
附:对于一组数据(u1,v1),(u2,v2),(u3,v3),…,(un,vn),其回归直线v=α+βu的斜率和截距的最小二乘估计分别为$\hat β=\frac{{\sum_{i=1}^n{({v_i}-\bar v)({u_i}-\bar u)}}}{{\sum_{i=1}^n{{{({u_i}-\bar u)}^2}}}},\hat α=\bar v-\hat β\bar u$.
5.已知等差数列{an}中,a3=4,a5=8,则a11=( )
| A. | 12 | B. | 16 | C. | 20 | D. | 24 |