题目内容
已知函数f(x)=
x2-2x,x∈(0,2],求f(x)的值域和单调区间.
| 1 |
| 2 |
考点:二次函数的性质
专题:计算题,函数的性质及应用
分析:化简f(x)=
x2-2x=
(x-2)2-2,从而确定函数的单调性,再求值域即可.
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:∵f(x)=
x2-2x=
(x-2)2-2,
∴f(x)在(0,2]上单调递减,
则
×4-2×2≤f(x)<0,
即-2≤f(x)<0,
故函数的值域为[-2,0).
| 1 |
| 2 |
| 1 |
| 2 |
∴f(x)在(0,2]上单调递减,
则
| 1 |
| 2 |
即-2≤f(x)<0,
故函数的值域为[-2,0).
点评:本题考查了二次函数的性质,属于基础题.

练习册系列答案
相关题目
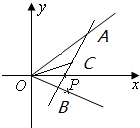 如图所示,射线OA、OB分别与x轴正半轴成45°和30°角,过点P(1,0)作直线AB分别交OA、OB于A、B两点,当AB的中点C恰好落在直线y=
如图所示,射线OA、OB分别与x轴正半轴成45°和30°角,过点P(1,0)作直线AB分别交OA、OB于A、B两点,当AB的中点C恰好落在直线y= 如图,在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,PA⊥平面ABCD,PA=AB,M、N分别是线段PB、AC上的动点,且不与端点重合,PM=AN.
如图,在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,PA⊥平面ABCD,PA=AB,M、N分别是线段PB、AC上的动点,且不与端点重合,PM=AN.