题目内容
向量
=（2sinx，cosx），
=（
cosx，2cosx），设函数f（x）=m
•
+n（其中m＞0，n∈R），函数f（x）在区间[0，
]上的值域为[2，3]．
（Ⅰ）求m，n的值，并求函数f（x）图象的单调递增区间；
（Ⅱ）在△ABC中，角A、B、C所对的边长分别为a、b、c，若f（A）=2，sinB=3sinC，△ABC的面积为
，求a．
| a |
| b |
| 3 |
| a |
| b |
| π |
| 4 |
（Ⅰ）求m，n的值，并求函数f（x）图象的单调递增区间；
（Ⅱ）在△ABC中，角A、B、C所对的边长分别为a、b、c，若f（A）=2，sinB=3sinC，△ABC的面积为
3
| ||
| 4 |
考点：平面向量数量积的运算,正弦定理
专题：平面向量及应用
分析：（1）首先由已知向量的运算得到f（x）的解析式，然后化简并求其性质．
（2）由f（A）=1，求得sin（2A+
）=
，解得A的值．因为sinB=3sinC，由正弦定理求得b=3c．因为△ABC面积为
，求得bc=3．由此解得b和c的值，再由余弦定理求得a的值．
（2）由f（A）=1，求得sin（2A+
| π |
| 6 |
| 1 |
| 2 |
3
| ||
| 4 |
解答：
解：由已知f（x）=m
•
+n=m（2
sinxcosx+2cos2x）+n=m（
sin2x+cos2x+1）+n=2msin（2x+
）+m+n，
（1）因为函数f（x）在区间[0，
]上的值域为[2，3]，m＞0．
所以（2x+
）∈[
，
]，所以3m+n=3，2m+n=2，解得m=1，n=0；
函数f（x）图象的单调递增区间-
+2kπ＜2x+
＜
+2kπ，即-
+kπ＜x＜
+kπ，k∈Z；
所以函数f（x）图象的单调递增区间（-
+kπ，
+kπ），k∈Z；
（2）f（A）=2，sinB=3sinC，△ABC的面积为
，
所以2sin（2A+
）+1=2，所以即sin（2A+
）=
，解得A=0（舍去）或A=
．
因为sinB=3sinC，由
=
=
，所以b=3c．-----①
因为△ABC面积为
，所以S=
bcsinA，即bc=3．-----②
由①和②解得b=3，c=1．
因为a2=b2+c2-2bc•cosA=32+12-2×3×1×cos
，
所以a=
．
| a |
| b |
| 3 |
| 3 |
| π |
| 6 |
（1）因为函数f（x）在区间[0，
| π |
| 4 |
所以（2x+
| π |
| 6 |
| π |
| 6 |
| 2π |
| 3 |
函数f（x）图象的单调递增区间-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
| π |
| 3 |
所以函数f（x）图象的单调递增区间（-
| π |
| 3 |
| π |
| 3 |
（2）f（A）=2，sinB=3sinC，△ABC的面积为
3
| ||
| 4 |
所以2sin（2A+
| π |
| 6 |
| π |
| 6 |
| 1 |
| 2 |
| π |
| 3 |
因为sinB=3sinC，由
| a |
| sinA |
| b |
| sinB |
| c |
| sinC |
因为△ABC面积为
3
| ||
| 4 |
| 1 |
| 2 |
由①和②解得b=3，c=1．
因为a2=b2+c2-2bc•cosA=32+12-2×3×1×cos
| π |
| 3 |
所以a=
| 7 |
点评：本题考查向量知识的运用，考查三角函数的化简与三角函数的性质，考查余弦定理的运用，正确化简函数是关键．
练习册系列答案
相关题目
若a=30.2，b=logπ3，c=log3cos
π，则（ ）
| ||
| 4 |
| A、b＞c＞a |
| B、b＞a＞c |
| C、a＞b＞c |
| D、c＞a＞b |
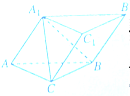如图，在三棱柱ABC-A1B1C1中，四边形A1ABB1为菱形，四边形BCC1B1为矩形，若AB⊥BC且AB=4，BC=3，∠A1AB=60°
如图，在三棱锥P-ABC中，已知平面PBC⊥平面ABC．