题目内容
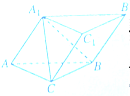 如图,在三棱柱ABC-A1B1C1中,四边形A1ABB1为菱形,四边形BCC1B1为矩形,若AB⊥BC且AB=4,BC=3,∠A1AB=60°
如图,在三棱柱ABC-A1B1C1中,四边形A1ABB1为菱形,四边形BCC1B1为矩形,若AB⊥BC且AB=4,BC=3,∠A1AB=60°(1)求证:平面CA1B⊥平面A1ABB1
(2)求直线A1C与平面BCC1B1所成的角的正切值.
考点:直线与平面所成的角,平面与平面垂直的判定
专题:空间角
分析:(1)由已知得B1B⊥CB,AB⊥CB,从而CB⊥AB1,再由A1B⊥AB1,能证明平面CA1B⊥平面A1ABB1.
(2)过A1作A1D⊥B1B于D,连接DC,∠A1CD为直线A1C与平面BCC1B1所成的角,由此能求出直线A1C与平面BCC1B1所成的角的正切值.
(2)过A1作A1D⊥B1B于D,连接DC,∠A1CD为直线A1C与平面BCC1B1所成的角,由此能求出直线A1C与平面BCC1B1所成的角的正切值.
解答:
(1)证明:∵四边形BCC1B1为矩形,∴B1B⊥CB,
又AB⊥CB,B1B∩AB=B
∴CB⊥面A1ABB1,AB1?A1ABB1,
∴CB⊥AB1,
∵四边形A1ABB1为菱形,∴A1B⊥AB1,且CB∩A1B=B,
∴AB1⊥平面A1CB,∵AB1?平面A1ABB1,
∴平面CA1B⊥平面A1ABB1.
(2)解:过A1作A1D⊥B1B于D,连接DC,∵BC⊥平面A1ABB1,
∴BC⊥A1D.∵BC∩BB1=B,∴A1D⊥平面BCC1B1,
故∠A1CD为直线A1C与平面BCC1B1所成的角.
在矩形BCC1B1中,DC=
,.
∵四边形A1ABB1是菱形,∠A1AB=60°,
AB=4,∴A1D=2
,
∴tan∠A1CD=
=
=
.
又AB⊥CB,B1B∩AB=B
∴CB⊥面A1ABB1,AB1?A1ABB1,
∴CB⊥AB1,
∵四边形A1ABB1为菱形,∴A1B⊥AB1,且CB∩A1B=B,
∴AB1⊥平面A1CB,∵AB1?平面A1ABB1,
∴平面CA1B⊥平面A1ABB1.

(2)解:过A1作A1D⊥B1B于D,连接DC,∵BC⊥平面A1ABB1,
∴BC⊥A1D.∵BC∩BB1=B,∴A1D⊥平面BCC1B1,
故∠A1CD为直线A1C与平面BCC1B1所成的角.
在矩形BCC1B1中,DC=
| 13 |
∵四边形A1ABB1是菱形,∠A1AB=60°,
AB=4,∴A1D=2
| 3 |
∴tan∠A1CD=
| A1D |
| CD |
2
| ||
|
2
| ||
| 13 |
点评:本题考查面面垂直的证明,考查线面角的正切值的求法,是中档题,解题时要注意空间思维能力的培养.

练习册系列答案
相关题目
设集合A={x|x2-5x+4<0},B={y|-1<y<3},则A∩(∁RB)=( )
| A、(1,4) |
| B、[3,4) |
| C、(1,3) |
| D、(1,2)∪(3,4) |
 (理) 如图,四棱锥S-ABCD中,底面ABCD为正方形,SA⊥平面ABCD,AB=3,SA=4
(理) 如图,四棱锥S-ABCD中,底面ABCD为正方形,SA⊥平面ABCD,AB=3,SA=4