题目内容
已知向量
、
满足|
|=1,
=(λ,2),且
⊥
,则|λ|的最小值是 .
| a |
| b |
| a |
| b |
| a |
| b |
考点:数量积判断两个平面向量的垂直关系
专题:平面向量及应用
分析:设
=(x,y),由题意可得λ2=
-4+
,由0≤y2<1和不等式的性质可得.
| a |
| 4y2 |
| 1-y2 |
| 4 |
| 1-y2 |
解答:
解:∵向量
、
满足|
|=1,
=(λ,2),
∴设
=(x,y),则x2+y2=1,
又∵
⊥
,∴
•
=λx+2y=0,
当λ≠0时,x=-
,
∴
+y2=1,解得λ2=
=
=-4+
,
∵0≤y2<1,∴0<1-y2≤1,
∴
≥4,∴-4+
≥0,
∴|λ|的最小值为0
故答案为:0
| a |
| b |
| a |
| b |
∴设
| a |
又∵
| a |
| b |
| a |
| b |
当λ≠0时,x=-
| 2y |
| λ |
∴
| 4y2 |
| λ2 |
| 4y2 |
| 1-y2 |
=
| -4(1-y2)+4 |
| 1-y2 |
| 4 |
| 1-y2 |
∵0≤y2<1,∴0<1-y2≤1,
∴
| 4 |
| 1-y2 |
| 4 |
| 1-y2 |
∴|λ|的最小值为0
故答案为:0
点评:本题考查平面向量的数量积与垂直关系,涉及不等式的性质,属基础题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
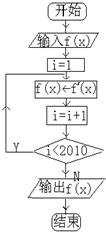
程序框图如图所示,该程序运行后输出的S的值是( )


A、
| ||
| B、-3 | ||
C、-
| ||
| D、2 |
设函数f(x)=x•ecosx(x∈[-π,π])的图象大致是( )
A、 |
B、 |
C、 |
D、 |