Question

如图，在三棱锥P-ABC中，已知平面PBC⊥平面ABC．
（1）若AB⊥BC，CP⊥PB，求证：CP⊥PA：
（2）若过点A作直线l上平面ABC，求证：l∥平面PBC．

Answer 1

考点：直线与平面平行的判定,空间中直线与直线之间的位置关系

专题：空间位置关系与距离

分析：（1）由已知得AB⊥平面PBC，从而CP⊥AB，又CP⊥PB，从而CP⊥平面PAB，由此得到CP⊥PA．
（2）在平面PBC内过点P作PD⊥BC，垂足为D，由已知得PD⊥平面ABC，从而l∥PD，由此能证明l∥平面PBC．

解答： （1）证明：因为平面PBC⊥平面ABC，平面PBC∩平面ABC=BC，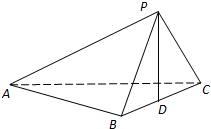
AB?平面ABC，AB⊥BC，所以AB⊥平面PBC． 
因为CP?平面PBC，所以CP⊥AB．
又因为CP⊥PB，且PB∩AB=B，AB，PB?平面PAB，
所以CP⊥平面PAB，
又因为PA?平面PAB，所以CP⊥PA．
（2）证明：在平面PBC内过点P作PD⊥BC，垂足为D．
因为平面PBC⊥平面ABC，
又平面PBC∩平面ABC=BC，PD?平面PBC，所以PD⊥平面ABC．
又l⊥平面ABC，所以l∥PD．
又l?平面PBC，PD?平面PBC，所以l∥平面PBC．

点评：本题考查异面直线垂直的证明，考查直线与平面平行的证明，解题时要认真审题，注意空间思维能力的培养．