题目内容
在R上定义运算?：x?y=x（1-y），若不等式（x-a）?（x+a）＜1对任意的实数x成立，则a的取值范围是 ．
考点：其他不等式的解法
专题：不等式的解法及应用
分析：根据定义，结合不等式恒成立即可得到结论．
解答：
解：由定义得不等式（x-a）?（x+a）＜1对任意的实数x成立，
等价为（x-a）（1-x-a）＜1对任意的实数x成立，
即x2-x+1+a-a2＞0恒成立，
则判别式△=1-4（1+a-a2）＜0，
即4a2-4a-3＜0，
解得-
＜a＜
，
故答案为：(-
，
)
等价为（x-a）（1-x-a）＜1对任意的实数x成立，
即x2-x+1+a-a2＞0恒成立，
则判别式△=1-4（1+a-a2）＜0，
即4a2-4a-3＜0，
解得-
| 1 |
| 2 |
| 3 |
| 2 |
故答案为：(-
| 1 |
| 2 |
| 3 |
| 2 |
点评：本题主要考查不等式的求解，根据定义结合一元二次不等式的解法是解决本题的关键．
练习册系列答案
相关题目
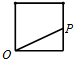
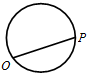
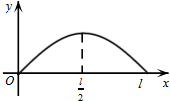点P从O点出发，按逆时针方向沿周长为l的图形运动一周，O、P两点间的距离y与点P所走路程x的函数关系如图，那么点P所走的图形是（ ）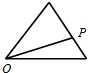
（理） 如图，四棱锥S-ABCD中，底面ABCD为正方形，SA⊥平面ABCD，AB=3，SA=4如果直线a和b没有公共点，那么a与b（ ）
| A、共面 |
| B、平行 |
| C、可能平行，也可能是异面直线 |
| D、是异面直线 |
（-8） -
=（ ）
| 1 |
| 3 |
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|