题目内容
已知等差数列{an},公差d≠0,a1=2,且a1,a3,a9成等比数列.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)求数列{2 an-1}的前n项和Sn.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)求数列{2 an-1}的前n项和Sn.
考点:数列的求和,等差关系的确定
专题:等差数列与等比数列
分析:(Ⅰ)由已知条件利用等差数列的通项公式和等比数列的性质,求出首项与公差,由此能求出an=2n.
(Ⅱ)数列{2an-1}的通项为2an-1=22n-1=4n-1,由此能求出数列{2 an-1}的前n项和Sn.
(Ⅱ)数列{2an-1}的通项为2an-1=22n-1=4n-1,由此能求出数列{2 an-1}的前n项和Sn.
解答:
解:(Ⅰ)由题意知a32=a1a9,
即 (2+2 d)2=2×(2+8d)…(3分)
得:d2-2d=0,
解得d=2或d=0(舍)∴an=2n.…(5分)
(Ⅱ)数列{2an-1}的通项为2an-1=22n-1=4n-1,…(7分)
∴Sn=41+42+43+…+4n-n=
×(4n-1)-n. …(10分)
即 (2+2 d)2=2×(2+8d)…(3分)
得:d2-2d=0,
解得d=2或d=0(舍)∴an=2n.…(5分)
(Ⅱ)数列{2an-1}的通项为2an-1=22n-1=4n-1,…(7分)
∴Sn=41+42+43+…+4n-n=
| 4 |
| 3 |
点评:本题考查数列的通项公式和前n项和的求法,解题时要认真审题,注意等差数列和等比数列的性质的灵活运用.

练习册系列答案
相关题目
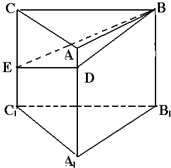 如图,已知体积为8,高为4的三棱柱ABC-A1B1C1,CC1⊥平面A1B1C1,点D、E分别在棱AA1和CC1上,且DE⊥B1C1,DA1=3,EC1=2.
如图,已知体积为8,高为4的三棱柱ABC-A1B1C1,CC1⊥平面A1B1C1,点D、E分别在棱AA1和CC1上,且DE⊥B1C1,DA1=3,EC1=2.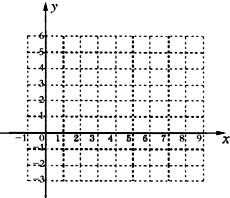 设函数f(x)=Asin(ωx+φ)+B(A>0,ω>0,|φ|<
设函数f(x)=Asin(ωx+φ)+B(A>0,ω>0,|φ|< 如图,斜三棱柱ABC-A1B1C1的所有棱长均为a,侧面B1C1CB⊥底面ABC,且AC1⊥BC.
如图,斜三棱柱ABC-A1B1C1的所有棱长均为a,侧面B1C1CB⊥底面ABC,且AC1⊥BC.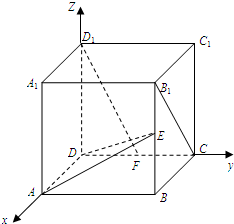 如图,在正方体ABCD-A1B1C1D1中,AB=2,E,F分别是BB1,CD的中点,(如图建立空间直角坐标系)
如图,在正方体ABCD-A1B1C1D1中,AB=2,E,F分别是BB1,CD的中点,(如图建立空间直角坐标系)