Question

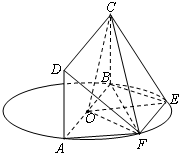如图，AB为圆O的直径，点E、F在圆O上，矩形ABCD所在平面和圆O所在的平面互相垂直，且AB=2，AD=EF=1．
（1）求证：AF⊥平面CBF；
（2）点G在线段CE上运动，当二面角O-AF-G的平面角的正弦值为

2 3

61

时，
①问点G的位置；
②求直线AG与平面CBE所成的角的正弦值．

Answer 1

考点：与二面角有关的立体几何综合题,直线与平面垂直的判定,直线与平面所成的角,点、线、面间的距离计算

专题：空间角

分析：（1）欲证AF⊥平面CBF，根据直线与平面垂直的判定定理可知只需证AF与平面CBF内两相交直线垂直，根据面面垂直的性质可知CB⊥平面ABEF，而AF?平面ABEF，则AF⊥CB，而AF⊥BF，满足定理所需条件．
（2）①过点F作FH⊥AB交AB于H，以H为原点，OH为x轴，HF为y轴，过H平行于AD的直线为z轴，建立空间直角坐标系，利用向量法能求出CG=

1

4

CE．
②由①知G（-

11

8

，

3

8

，

3

4

），

AG

=（-

15

8

，

3

8

，

3

4

），求出平面CBE的法向量，利用向量法能求出直线AG与平面CBE所成的角的正弦值．

解答： （1）证明：∵平面ABCD⊥平面ABEF，CB⊥AB，
平面ABCD∩平面ABEF=AB，
∴CB⊥平面ABEF∵AF?平面ABEF，
∴AF⊥CB，
又AB为圆O的直径，∴AF⊥BF，
∴AF⊥平面CBF．
（2）①过点F作FH⊥AB交AB于H，
DA⊥圆面O，FH?圆面O，DA⊥FH，
∴FH⊥平面ABCD，
∴∠FBA是BF与平面ABCD所成角的平面角，
∵AB=2，AD=EF=1，∴HF=

3

2

，BH=

3

2

，
∴∠FBA=30°，∴AF=1，∴BE=1，
由题意，以H为原点，OH为x轴，HF为y轴，过H平行于AD的直线为z轴，
建立空间直角坐标系，
则A（

1

2

，0，0），F（0，

3

2

，0），O（-

1

2

，0，0），C（-

3

2

，0，1），E（-1，

3

2

，0），
设G（a，b，c），

CG

=λ

CE

，则（a+

3

2

，b，c-1）=（

1

2

λ，

3

2

λ，-λ），
∴G（

1

2

λ-

3

2

，

3

2

λ，1-λ），
∴

AF

=(-

1

2

，

3

2

，0)，

AG

=（

1

2

λ-2，

3

2

λ，1-λ），
设平面AFG的法向量

m

=(x，y，z)，
则

m • AF =- 1 2 x+ 3 2 y=0 m • AG =( 1 2 λ-2)x+ 3 2 λy+(1-λ)z=0

，
取x=

3

，得

m

=（

3

，1，

3 λ-2 3

λ-1

），
∵平面OAF的法向量为

n

=（0，0，1），
二面角O-AF-G的平面角的正弦值为

2 3

61

，
∴cos＜

m

，

n

＞=

3 λ-2 3 λ-1

4+( 3 λ-2 3 λ-1 )2

=

1-( 2 3 61 )2

，
解得λ=

1

4

，∴CG=

1

4

CE．
②由①知G（-

11

8

，

3

8

，

3

4

），
∴

AG

=（-

15

8

，

3

8

，

3

4

），
∵B（-

3

2

，0，0），C（-

3

2

，0，1），E（-1，

3

2

，0），
∴

BC

=（0，0，1），

BE

=(

1

2

，

3

2

，0)，
设平面CBE的法向量

n

=（x，y，z），
则

n • BC =z=0 n • BE = 1 2 x+ 3 2 y=0

，
取x=

3

，得

n

=(

3

，-1，0)，
设直线AG与平面CBE所成的角为θ，
则sinθ=|cos＜

AG

，

n

＞|=|

- 15 8 3 - 3 8

2• 225 64 + 3 64 + 9 16

|=

2 22

11

．
∴直线AG与平面CBE所成的角的正弦值为

2 22

11

．

点评：本题考查直线与平面垂直的证明，考查满足条件的点的位置的确定，考查直线与平面所成角的正弦值的求法，解题时要认真审题，注意向量法的合理运用．