题目内容
抛物线y=x2在A（1，1）处的切线与x轴及该抛物线所围成的图形面积为 ．
考点：定积分在求面积中的应用
专题：导数的综合应用
分析：求出函数的切线方程，利用积分的几何意义即可求出区域的面积．
解答：
解：函数的导数为f′（x）=2x，
则在（1，1）处的切线斜率k=f′（1）=2，
则对应的切线方程为y-1=2（x-1），即y=2x-1，
令y=0，得x=
，
则由积分的几何意义可得阴影部分的面积S=
(x2-(2x-1))dx-
×
×1=
-
=
，
故答案为：
．
解：函数的导数为f′（x）=2x，则在（1，1）处的切线斜率k=f′（1）=2，
则对应的切线方程为y-1=2（x-1），即y=2x-1，
令y=0，得x=
| 1 |
| 2 |
则由积分的几何意义可得阴影部分的面积S=
| ∫ | 1 0 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 12 |
故答案为：
| 1 |
| 12 |
点评：本题主要考查导数的应用，利用导数的几何意义求出切线方程，以及利用积分求区域面积是解决本题的关键．
练习册系列答案
相关题目
已知双曲线
-
=1（a＞0，b＞0）的渐近线与实轴的夹角为45°，则双曲线的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
B、
| ||
C、
| ||
D、2
|
命题p：a≥1；命题q：关于x的实系数方程x2-2
x+a=0有虚数解，则p是q的（ ）
| 2 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
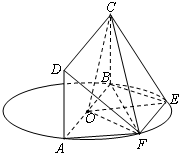如图，AB为圆O的直径，点E、F在圆O上，矩形ABCD所在平面和圆O所在的平面互相垂直，且AB=2，AD=EF=1．