题目内容
求使函数y=1-
cos
x(x∈R)取得最大值、最小值的自变量x的集合,并分别写出最大值、最小值.
| 1 |
| 2 |
| π |
| 3 |
考点:余弦函数的定义域和值域
专题:三角函数的图像与性质
分析:根据余弦函数的图象和性质即可得到结论.
解答:
解:∵-1≤cos
x≤1,
∴当cos
x=1时,函数y取得最小值y=1-
=
,此时
x=2kπ,即x=6k,k∈Z.
当cos
x=-1时,函数y取得最大值y=1+
=
,此时
x=2kπ-π,即x=6k-3,k∈Z.
即函数取值最小值的集合为{x|x=6k,k∈Z},
函数取值最大值的集合为{x|x=6k-3,k∈Z}.
| π |
| 3 |
∴当cos
| π |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 3 |
当cos
| π |
| 3 |
| 1 |
| 2 |
| 3 |
| 2 |
| π |
| 3 |
即函数取值最小值的集合为{x|x=6k,k∈Z},
函数取值最大值的集合为{x|x=6k-3,k∈Z}.
点评:本题主要考查三角函数的最值,利用余弦函数的图象和性质是解决本题的关键,比较基础.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
命题p:a≥1;命题q:关于x的实系数方程x2-2
x+a=0有虚数解,则p是q的( )
| 2 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
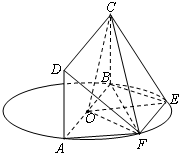 如图,AB为圆O的直径,点E、F在圆O上,矩形ABCD所在平面和圆O所在的平面互相垂直,且AB=2,AD=EF=1.
如图,AB为圆O的直径,点E、F在圆O上,矩形ABCD所在平面和圆O所在的平面互相垂直,且AB=2,AD=EF=1.