题目内容
将函数f（x）=
sin2x+cos2x（x∈R）的图象向左平移
个单位长度后得到函数y=g（x），则函数y=g（x）（ ）
| 3 |
| π |
| 6 |
| A、是奇函数 |
| B、是偶函数 |
| C、既是奇函数又是偶函数 |
| D、既不是奇函数，也不是偶函数 |
考点：函数y=Asin（ωx+φ）的图象变换
专题：三角函数的图像与性质
分析：化简函数的表达式，然后图象向左平移
个单位得到函数g（x）的表达式的图象，即可得到函数的表达式，然后判定奇偶性．
| π |
| 6 |
解答：
解：函数f（x）=
sin2x+cos2x=2sin（2x+
），图象向左平移
个单位得到函数y=g（x）的图象，
所以函数g（x）=2sin（2x+
）=2cos2x，
∴函数y=g（x）是偶函数．
故选：B．
| 3 |
| π |
| 6 |
| π |
| 6 |
所以函数g（x）=2sin（2x+
| π |
| 2 |
∴函数y=g（x）是偶函数．
故选：B．
点评：本题是基础题，考查三角函数的化简求值，图象的平移，函数奇偶性的判定，考查计算能力．
练习册系列答案
相关题目
已知双曲线
-
=1（a＞0，b＞0）的渐近线与实轴的夹角为45°，则双曲线的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
B、
| ||
C、
| ||
D、2
|
命题p：a≥1；命题q：关于x的实系数方程x2-2
x+a=0有虚数解，则p是q的（ ）
| 2 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
函数y=|x|在x=0处的导数是（ ）
| A、0 | B、不存在 | C、1 | D、-1 |
函数y=2sin（
-2x）（其中0≤x≤π）为增函数的区间是（ ）
| π |
| 6 |
A、（0，
| ||||
B、（
| ||||
C、（
| ||||
D、（
|
设x＞0，y＞0，且2x+y=6，则9x+3y有（ ）
| A、最大值27 |
| B、最小值27 |
| C、最大值54 |
| D、最小值54 |
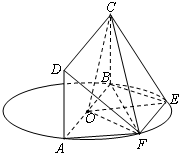如图，AB为圆O的直径，点E、F在圆O上，矩形ABCD所在平面和圆O所在的平面互相垂直，且AB=2，AD=EF=1．