题目内容
已知函数f(x)=lnx-
,是否存在过点(1,-1)的直线与函数y=f(x)的图象相切?若存在,有多少条?若不存在,请说明理由.
| x-1 |
| x |
考点:利用导数研究曲线上某点切线方程
专题:综合题,导数的综合应用
分析:假设存在满足条件的直线与函数相切,根据导数的几何意义,求出切线方程,结合导数的知识推导.
解答:
解:假设存在这样的切线,设其中一个切点T(x0,lnx0-
),
∴切线方程:y+1=
(x-1),将点T坐标代入得:lnx0-
=
,
即lnx0+
-
-1=0,①
设g(x)=lnx+
-
-1,则g′(x)=
.
令g'(x)=0,则x=1或x=2.
∴g(x)在区间(0,1),(2,+∞)上是增函数,在区间(1,2)上是减函数,
∴g(x)在x=1处取得极大值g(1)=1,在x=2处取得极小值g(2)=ln2+
,
∴g(x)>0在[1,+∞)上恒成立,即g(x)=0在[1,+∞)上无解.
∵g(
)=-ln4-3<0,g(1)=1>0,g(x)在区间(0,1)上单调递增,
根据零点定理,g(x)在区间(0,1)上有且仅有一个实数根,即方程①有且仅有一解,
故符合条件的切线有且仅有一条.
| x0-1 |
| x0 |
∴切线方程:y+1=
| x0-1 |
| x02 |
| x0-1 |
| x0 |
| (x0-1)2 |
| x02 |
即lnx0+
| 3 |
| x0 |
| 1 |
| x02 |
设g(x)=lnx+
| 3 |
| x |
| 1 |
| x2 |
| (x-1)(x-2) |
| x3 |
令g'(x)=0,则x=1或x=2.
| x | (0,1) | 1 | (1,2) | 2 | (2,+∞) |
| g'(x) | + | 0 | - | 0 | + |
| g(x) | 递增 | 极大值 | 递减 | 极小值 | 递增 |
∴g(x)在x=1处取得极大值g(1)=1,在x=2处取得极小值g(2)=ln2+
| 1 |
| 4 |
∴g(x)>0在[1,+∞)上恒成立,即g(x)=0在[1,+∞)上无解.
∵g(
| 1 |
| 4 |
根据零点定理,g(x)在区间(0,1)上有且仅有一个实数根,即方程①有且仅有一解,
故符合条件的切线有且仅有一条.
点评:本题考查了导数的应用,考查利用导数研究函数单调区间,对于存在性问题,通常是先假设存在,由假设出发进行推导,若推出矛盾,说明假设错误,即不存在,反之说明存在.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
函数y=2sin(
-2x)(其中0≤x≤π)为增函数的区间是( )
| π |
| 6 |
A、(0,
| ||||
B、(
| ||||
C、(
| ||||
D、(
|
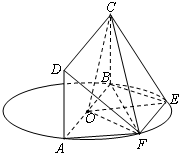 如图,AB为圆O的直径,点E、F在圆O上,矩形ABCD所在平面和圆O所在的平面互相垂直,且AB=2,AD=EF=1.
如图,AB为圆O的直径,点E、F在圆O上,矩形ABCD所在平面和圆O所在的平面互相垂直,且AB=2,AD=EF=1. 如图所示的茎叶图记录了甲、乙两组各四名同学的投篮命中次数,乙组记录中有一个数据模糊,无法确认,在图中以x表示.
如图所示的茎叶图记录了甲、乙两组各四名同学的投篮命中次数,乙组记录中有一个数据模糊,无法确认,在图中以x表示.