题目内容
在等比数列{an}中,已知a1=2,且a2,a1+a3,a4成等差数列.
(Ⅰ)求数列{an}的通项公式an;
(Ⅱ)设数列{an2-an}的前n项和为Sn,记bn=
,求数列{bn}的前n项和Tn.
(Ⅰ)求数列{an}的通项公式an;
(Ⅱ)设数列{an2-an}的前n项和为Sn,记bn=
| 2n |
| Sn |
考点:数列的求和,等比数列的通项公式,等比数列的前n项和,等差数列的性质
专题:计算题,等差数列与等比数列
分析:(Ⅰ)根据a2,a1+a3,a4成等差数列得到2(a1+a3)=a2+a4,应用等比数列通项公式,化简求出公比,写出通项an;
(Ⅱ)运用分组求和求出Sn,注意分成两组都是等比数列,并运用等比数列求和公式,然后求出bn,并对bn拆成两项的差,运用裂项相消求和即可求出Tn.
(Ⅱ)运用分组求和求出Sn,注意分成两组都是等比数列,并运用等比数列求和公式,然后求出bn,并对bn拆成两项的差,运用裂项相消求和即可求出Tn.
解答:
解:(Ⅰ)设等比数列的公比为q,由已知得:2(a1+a3)=a2+a4,
即2(a1+a1q2)=a1q+a1q3,解得q=2,
又∵a1=2,
∴an=a1qn-1=2n;
(Ⅱ)由(Ⅰ)得:
Sn=(a12+a22+a32+…+an2)-(a1+a2+…+an)
=(4+42+43+…+4n)-(2+22+23+…+2n)
=
-
=
(4n-1)-2(2n-1)=(2n-1)(
•2n-
)=
(2n-1)(2n+1-1),
又bn=
,
∴bn=
•
=
(
-
),
∴Tn=b1+b2+b3+…+bn-1+bn
=
[(
-
)+(
-
)+(
-
)+…+(
-
)
+(
-
)]
=
(1-
)=
-
.
即2(a1+a1q2)=a1q+a1q3,解得q=2,
又∵a1=2,
∴an=a1qn-1=2n;
(Ⅱ)由(Ⅰ)得:
Sn=(a12+a22+a32+…+an2)-(a1+a2+…+an)
=(4+42+43+…+4n)-(2+22+23+…+2n)
=
| 4(1-4n) |
| 1-4 |
| 2(1-2n) |
| 1-2 |
=
| 4 |
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
又bn=
| 2n |
| Sn |
∴bn=
| 3 |
| 2 |
| 2n |
| (2n-1)(2n+1-1) |
| 3 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1-1 |
∴Tn=b1+b2+b3+…+bn-1+bn
=
| 3 |
| 2 |
| 1 |
| 21-1 |
| 1 |
| 22-1 |
| 1 |
| 22-1 |
| 1 |
| 23-1 |
| 1 |
| 23-1 |
| 1 |
| 24-1 |
| 1 |
| 2n-1-1 |
| 1 |
| 2n-1 |
+(
| 1 |
| 2n-1 |
| 1 |
| 2n+1-1 |
=
| 3 |
| 2 |
| 1 |
| 2n+1-1 |
| 3 |
| 2 |
| 3 |
| 2n+2-2 |
点评:本题主要考查等比数列的通项公式与求和公式,以及等差数列的性质,考查两种数列求和方法:分组求和与裂项相消求和,这是两种重要的求和方法,务必掌握.

练习册系列答案
相关题目
已知双曲线
-
=1(a>0,b>0)的渐近线与实轴的夹角为45°,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
B、
| ||
C、
| ||
D、2
|
设x>0,y>0,且2x+y=6,则9x+3y有( )
| A、最大值27 |
| B、最小值27 |
| C、最大值54 |
| D、最小值54 |
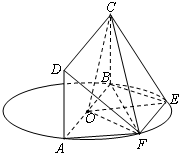 如图,AB为圆O的直径,点E、F在圆O上,矩形ABCD所在平面和圆O所在的平面互相垂直,且AB=2,AD=EF=1.
如图,AB为圆O的直径,点E、F在圆O上,矩形ABCD所在平面和圆O所在的平面互相垂直,且AB=2,AD=EF=1.