题目内容
若数列{an}满足:a1=
,an+1-an=
,求数列的通项公式an.
| 2 |
| 3 |
|
考点:数列递推式
专题:点列、递归数列与数学归纳法
分析:由首项和数列递推式求出a2,把递推式两边平方,取n=n+1得另一递推式,作差后得到新的等差数列
{an+1-an},求出其通项公式利用累加法求数列的通项公式an.
{an+1-an},求出其通项公式利用累加法求数列的通项公式an.
解答:
解:取n=1,得a2-a1=
,
又a1=
,
解得:a2=2.
由an+1-an=
,得
(an+1-an)2=
(an+1+an) ①
则(an+2-an+1)2=
(an+2+an+1) ②
②-①得:(an+2-an)(an+2-2an+1+an)=
(an+2-an),
由an+1-an=
知数列是递增数列,
∴an+2-an≠0,
∴an+2-2an+1+an=
,
即(an+2-an+1)-(an+1-an)=
.
∴数列{an+1-an}是以a2-a1=2-
=
为首项,以
为公差的等差数列.
则an+1-an=
+
(n-1)=
(n+1).
∴an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1
=
[n+(n-1)+(n-2)+…+2+1]=
•
=
.
|
又a1=
| 2 |
| 3 |
解得:a2=2.
由an+1-an=
|
(an+1-an)2=
| 2 |
| 3 |
则(an+2-an+1)2=
| 2 |
| 3 |
②-①得:(an+2-an)(an+2-2an+1+an)=
| 2 |
| 3 |
由an+1-an=
|
∴an+2-an≠0,
∴an+2-2an+1+an=
| 2 |
| 3 |
即(an+2-an+1)-(an+1-an)=
| 2 |
| 3 |
∴数列{an+1-an}是以a2-a1=2-
| 2 |
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
则an+1-an=
| 4 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
∴an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1
=
| 2 |
| 3 |
| 2 |
| 3 |
| (n+1)n |
| 2 |
| n(n+1) |
| 3 |
点评:本题考查数列递推式,考查了等差关系的确定,训练了利用累加法求数列的通项公式,是中档题.

练习册系列答案
相关题目
函数y=|x|在x=0处的导数是( )
| A、0 | B、不存在 | C、1 | D、-1 |
设x>0,y>0,且2x+y=6,则9x+3y有( )
| A、最大值27 |
| B、最小值27 |
| C、最大值54 |
| D、最小值54 |
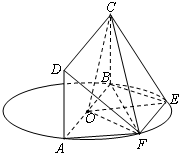 如图,AB为圆O的直径,点E、F在圆O上,矩形ABCD所在平面和圆O所在的平面互相垂直,且AB=2,AD=EF=1.
如图,AB为圆O的直径,点E、F在圆O上,矩形ABCD所在平面和圆O所在的平面互相垂直,且AB=2,AD=EF=1.