题目内容
已知函数f（x）=x2+f′（2）（lnx-x），则f′（1）=（ ）
| A、1 | B、2 | C、3 | D、4 |
考点：导数的运算
专题：导数的概念及应用
分析：f′（2）是一个常数，对函数f（x）求导，能直接求出f′（1）的值．
解答：
解：∵f（x）=x2+f′（2）（lnx-x），
∴f′（x）=2x+f′（2）（
-1）；
∴f′（1）=2×1+f′（2）×（1-1）=2．
故选：B．
∴f′（x）=2x+f′（2）（
| 1 |
| x |
∴f′（1）=2×1+f′（2）×（1-1）=2．
故选：B．
点评：本题考查了利用求导法则求函数的导函数问题，解题时应知f′（2）是一个常数，根据求导法则进行计算即可，是基础题．
练习册系列答案
优等生题库系列答案
53天天练系列答案
相关题目
已知集合 A={x|x2+x-2＜0}，B={-2，-1，0，1，2}，则A∩B=（ ）
| A、{-2，-1，0，1} |
| B、{-1，0，1} |
| C、{0，1} |
| D、{-1，0} |
已知等差数列{an}的首项a1=1，公差d=2，则a4=（ ）
| A、5 | B、6 | C、7 | D、9 |
甲、乙、丙3位志愿者安排在周一至周五的5天中参加某项志愿者活动，要求每人参加一天且每天至多安排一人，现要求甲安排在另外两位前面且丙不安排在周五，则不同的安排方法共有（ ）
| A、14种 | B、16种 |
| C、20种 | D、24种 |
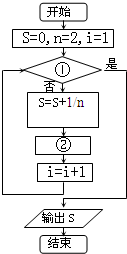
如图给出了计算
+
+
+…+
的值的程序框图，其中①②分别是（ ）
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 6 |
| 1 |
| 60 |
| A、i＜30，n=n+2 |
| B、i=30，n=n+2 |
| C、i＞30，n=n+2 |
| D、i＞30，n=n+1 |