题目内容
已知等差数列{an}的首项a1=1，公差d=2，则a4=（ ）
| A、5 | B、6 | C、7 | D、9 |
考点：等差数列的性质
专题：等差数列与等比数列
分析：由题意把已知数据代入等差数列的通项公式计算可得．
解答：
解：由等差数列的通项公式可得：
a4=a1+3d=1+3×2=7
故选：C
a4=a1+3d=1+3×2=7
故选：C
点评：本题考查等差数列的通项公式，属基础题．
练习册系列答案
相关题目
设函数f（x）=alnx+blgx+1，则f（1）+f（2）+…+f（2014）+f（
）+f（
）+…+f（
）=（ ）
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2014 |
| A、4028 | B、4027 |
| C、2014 | D、2013 |
设等差数列{an}的前n项和为Sn，若a2+a4+a9=24，则S9=（ ）
| A、36 | B、72 | C、144 | D、70 |
命题p：?x∈R，sinx-cosx＜
，命题q：“a=1”是“直线l1：ax+2y-1=0与直线l2：x+（a+1）y+4=0平行”的充分条件，则下列命题中，真命题是（ ）
| 2 |
| A、（￢q）∨p |
| B、p∧q |
| C、（￢p）∧（￢q） |
| D、（￢p）∨（￢q） |
i2014=（ ）
| A、-1 | B、1 | C、-i | D、i |
已知函数f（x）=x2+f′（2）（lnx-x），则f′（1）=（ ）
| A、1 | B、2 | C、3 | D、4 |
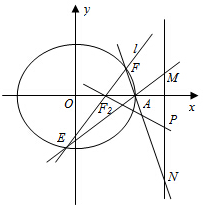已知椭圆C：