题目内容
已知sin（3π+α）=2sin（
+α），求下列各式的值．
（1）
；
（2）sin2α+sin2α．
| 3π |
| 2 |
（1）
| sinα-4cosα |
| 5sinα+2cosα |
（2）sin2α+sin2α．
考点：运用诱导公式化简求值,同角三角函数基本关系的运用
专题：三角函数的求值
分析：（1）已知等式两边利用诱导公式化简得到sinα=2cosα，代入原式计算即可得到结果；
（2）由sinα=2cosα，得到tanα的值，原式第二项利用二倍角的正弦函数公式化简，分母看做“1”，利用同角三角函数间基本关系变形，再分子分母除以cos2α，利用同角三角函数间基本关系化简，将tanα的值代入计算即可求出值．
（2）由sinα=2cosα，得到tanα的值，原式第二项利用二倍角的正弦函数公式化简，分母看做“1”，利用同角三角函数间基本关系变形，再分子分母除以cos2α，利用同角三角函数间基本关系化简，将tanα的值代入计算即可求出值．
解答：
解：（1）∵sin（3π+α）=2sin（
+α），
∴-sinα=-2cosα，即sinα=2cosα，
则原式=
=
=-
；
（2）∵sinα=2cosα，即tanα=2，
∴原式=
=
=
=
．
| 3π |
| 2 |
∴-sinα=-2cosα，即sinα=2cosα，
则原式=
| 2cosα-4cosα |
| 10cosα+2cosα |
| -2 |
| 12 |
| 1 |
| 6 |
（2）∵sinα=2cosα，即tanα=2，
∴原式=
| sin2α+2sinαcosα |
| sin2α+cos2α |
| tan2α+2tanα |
| tan2α+1 |
| 4+4 |
| 4+1 |
| 8 |
| 5 |
点评：此题考查了同角三角函数基本关系的运用，熟练掌握基本关系是解本题的关键．
练习册系列答案
相关题目
命题p：?x∈R，sinx-cosx＜
，命题q：“a=1”是“直线l1：ax+2y-1=0与直线l2：x+（a+1）y+4=0平行”的充分条件，则下列命题中，真命题是（ ）
| 2 |
| A、（￢q）∨p |
| B、p∧q |
| C、（￢p）∧（￢q） |
| D、（￢p）∨（￢q） |
已知函数f（x）=x2+f′（2）（lnx-x），则f′（1）=（ ）
| A、1 | B、2 | C、3 | D、4 |
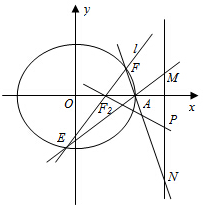已知椭圆C：