题目内容
11.给出下列命题:①零向量没有方向;②若两个空间向量相等,则它们的起点相同,终点也相同;③若空间向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$|=|$\overrightarrow{b}$|,则$\overrightarrow{a}$=$\overrightarrow{b}$;④若空间向量$\overrightarrow{m}$,$\overrightarrow{n}$,$\overrightarrow{p}$满足$\overrightarrow{m}$=$\overrightarrow{n}$,$\overrightarrow{n}$=$\overrightarrow{p}$,则$\overrightarrow{m}$=$\overrightarrow{p}$;⑤空间中任意两个单位向量必相等.其中正确命题的个数为( )| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
分析 ①,零向量有方向,是任意的;
②,向量相等,方向相同,大小相等即可;
③,若|$\overrightarrow{a}$|=|$\overrightarrow{b}$|,则$\overrightarrow{a}$、$\overrightarrow{b}$的方向没定;
④,根据向量相等的条件可判定;
⑤,空间中任意两个单位向量的模相等.方向没定,向量不一定等;
解答 解:对于①,零向量有方向,是任意的,故错;
对于②,若两个空间向量相等,方向相同,大小相等即可,故错;
对于③,若空间向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$|=|$\overrightarrow{b}$|,则$\overrightarrow{a}$、$\overrightarrow{b}$的方向没定,故错;
对于④,若空间向量$\overrightarrow{m}$,$\overrightarrow{n}$,$\overrightarrow{p}$满足$\overrightarrow{m}$=$\overrightarrow{n}$,$\overrightarrow{n}$=$\overrightarrow{p}$,则$\overrightarrow{m}$=$\overrightarrow{p}$,正确;
对于⑤,空间中任意两个单位向量的模相等.方向没定,向量不一定等,故错;
故选:D,
点评 那么题考查了空间向量的概念及性质,属于基础题.

练习册系列答案
相关题目
16.已知a=cos17°cos23°-sin17°sin23°,b=2cos225°-1,c=$\frac{{\sqrt{3}}}{2}$,则a,b,c的大小关系( )
| A. | b>a>c | B. | c>b>a | C. | c>a>b | D. | a>c>b |
20.在圆的方程x2+y2+Dx+Ey+F=0中,若D2=E2>4F,则圆的位置满足( )
| A. | 截两坐标轴所得弦的长度相等 | B. | 与两坐标轴都相切 | ||
| C. | 与两坐标轴相离 | D. | 上述情况都有可能 |
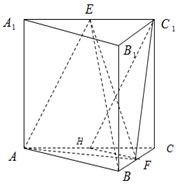 如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB=AC,E,F,H分别是A1C1,BC,AC的中点.
如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB=AC,E,F,H分别是A1C1,BC,AC的中点. 如图,在三棱椎P-ABC中,D,E,F分别是棱PC、AC、AB的中点,且PA⊥面ABC.
如图,在三棱椎P-ABC中,D,E,F分别是棱PC、AC、AB的中点,且PA⊥面ABC.