题目内容
13.若$α∈(0,\frac{π}{2})$,且${sin^2}α+cos2α=\frac{1}{4}$,则tanα的值等于( )| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | 1 | D. | $\sqrt{3}$ |
分析 把已知的等式中的cos2α,利用同角三角函数间的基本关系化简后,得到关于sinα的方程,根据α的度数,求出方程的解即可得到sinα的值,然后利用特殊角的三角函数值,由α的范围即可得到α的度数,利用α的度数求出tanα即可.
解答 解:由cos2α=1-2sin2α,得到sin2α+cos2α=1-sin2α=$\frac{1}{4}$,
则sin2α=$\frac{3}{4}$,又α∈(0,$\frac{π}{2}$),
所以sinα=$\frac{\sqrt{3}}{2}$,
则α=$\frac{π}{3}$,
所以tanα=tan$\frac{π}{3}$=$\sqrt{3}$.
故选:D.
点评 此题考查学生灵活运用二倍角的余弦函数公式及同角三角函数间的基本关系化简求值,学生做题时应注意角度的范围,属于基础题.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
3.设集合M={x|x2-3x-4≤0},N={x||x-3|<1},则M∩N=( )
| A. | (2,4) | B. | (2,4] | C. | [2,4] | D. | (-1,4] |
4.在下列各函数中,偶函数是( )
| A. | y=x3 | B. | y=x4 | C. | y=$\sqrt{x}$ | D. | y=$\frac{1}{x}$ |
8.若直线y=2x与双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)有公共点,则双曲线的离心率的取值范围为( )
| A. | (1,$\sqrt{5}$) | B. | ($\sqrt{5}$,+∞) | C. | (1,$\sqrt{5}$] | D. | [$\sqrt{5}$,+∞) |
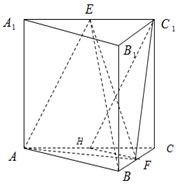 如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB=AC,E,F,H分别是A1C1,BC,AC的中点.
如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB=AC,E,F,H分别是A1C1,BC,AC的中点. 如图,在三棱椎P-ABC中,D,E,F分别是棱PC、AC、AB的中点,且PA⊥面ABC.
如图,在三棱椎P-ABC中,D,E,F分别是棱PC、AC、AB的中点,且PA⊥面ABC.