题目内容
19．抛物线y=x2-4x+3与x轴围成的封闭图形的面积为（ ）| A． | $\frac{2}{3}$ | B． | $\frac{4}{3}$ | C． | 2 | D． | $\frac{8}{3}$ |
分析 由x2-4x+3=0，得x=1，x=3再由图形可知求出x从1到3，x2-4x+3上的定积分即为抛物线y=x2-4x+3与x轴围成的封闭图形的面积．
解答 解：由x2-4x+3=0，得x=1，x=3，
∴抛物线y=x2-4x+3与x轴围成的封闭图形的面积为S=-${∫}_{1}^{3}$（x2-4x+3）dx=-（$\frac{1}{3}$x3-2x2+3x）|${\;}_{1}^{3}$=-[（9-18+9）-（$\frac{1}{3}$-2+3）]=$\frac{4}{3}$
故选：B
点评 考查学生会利用定积分求平面图形面积．会利用数形结合的数学思想来解决实际问题．
练习册系列答案
特高级教师点拨系列答案
相关题目
9．若$2sin（{θ+\frac{π}{3}}）=3sin（{\frac{π}{3}-θ}）$，则tanθ=（ ）
| A． | $-\frac{{\sqrt{3}}}{2}$ | B． | $\frac{{\sqrt{3}}}{5}$ | C． | $\frac{{2\sqrt{3}}}{3}$ | D． | $2\sqrt{3}$ |
7．设x．y满足约束条件$\left\{\begin{array}{l}{2x+y-3≤0}\\{2x-2y-1≤0}\\{x-a≥0}\end{array}\right.$，若$\frac{x-y}{x+y}$的最大值为2，则a的值为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{4}$ | C． | $\frac{3}{8}$ | D． | $\frac{5}{9}$ |
14．已知四棱锥P-ABCD中，$\overrightarrow{AB}=（{4，-2，3}）$，$\overrightarrow{AD}=（{-4，1，0}）$，$\overrightarrow{AP}=（{-6，2，-8}）$，则点P到底面ABCD的距离为（ ）
| A． | $\frac{{\sqrt{26}}}{13}$ | B． | $\frac{{\sqrt{26}}}{26}$ | C． | 1 | D． | 2 |
11．已知a，b，c∈（0，+∞），则下列三个数$a+\frac{4}{b}$，$b+\frac{9}{c}$，$c+\frac{16}{a}$（ ）
| A． | 都大于6 | B． | 至少有一个不大于6 | ||
| C． | 都小于6 | D． | 至少有一个不小于6 |
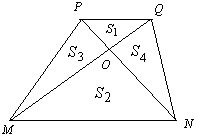如图，在梯形PMNQ中，PQ∥MN，对角线PN和MQ相交于点O，并把梯形分成四部分，记这四部分的面积分别为S1，S2，S3，S4．试判断S1+S2和S3+S4的大小关系，并证明你的结论．