题目内容
4．某棱柱的三视图如图示，则该棱柱的体积为（ ）
| A． | 3 | B． | 4 | C． | 6 | D． | 12 |
分析 由已知中的三视图可得：该几何体上部是一个以俯视图为底面四棱柱，进而可得答案．
解答 
解：由已知中的三视图可得：该几何体上部是一个以俯视图为底面四棱柱，
棱柱的底面面积S=$\frac{1}{2}$×（2+4）×2=6，
棱柱的高为1，
故棱柱的体积V=6．
故选：C．
点评 本题考查的知识点是由三视图，求体积和表面积，根据已知的三视图，判断几何体的形状是解答的关键．
练习册系列答案
相关题目
14．设甲、乙两楼相距10m，从乙楼底望甲楼顶的仰角为60°，从甲楼顶望乙楼顶的俯角为30°，则甲、乙两楼的高分别是（ ）
| A． | $\frac{10\sqrt{3}}{3}$m，$\frac{40}{3}$$\sqrt{3}$ m | B． | 10$\sqrt{3}$ m，20$\sqrt{3}$ m | C． | 10（$\sqrt{3}$-$\sqrt{2}$） m，20$\sqrt{3}$ m | D． | 10$\sqrt{3}$ m，$\frac{40}{3}$$\sqrt{3}$ m |
如图，渔船甲位于岛屿A的南偏西60°方向的B处，且与岛屿A相距6海里，渔船乙以5 海里/小时的速度从岛屿A出发沿正北方向航行，若渔船甲同时从B处出发沿北偏东α的方向追赶渔船乙，刚好用2小时追上．
12．${∫}_{-π}^{π}$sin2$\frac{x}{2}$dx=（ ）
| A． | 0 | B． | π-1 | C． | π | D． | π+1 |
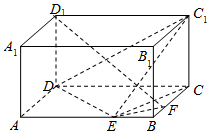如图，在长方体ABCD-A1B1C1D1中，已知AB=4，AD=3，AA1=2．E、F分别是线段AB、BC上的点，且EB=FB=1．
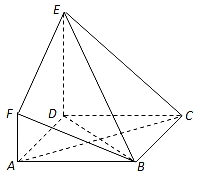如图，ABCD是边长为3的正方形，DE⊥平面ABCD，AF∥DE，DE=3AF，BE与平面ABCD所成角为60°．
14．将函数y=sin2x的图象向右平移$\frac{π}{6}$个单位，得到函数y=f（x）的图象，则f（x）=（ ）
| A． | $cos（2x-\frac{π}{6}）$ | B． | $sin（2x-\frac{π}{6}）$ | C． | $cos（2x-\frac{π}{3}）$ | D． | $sin（2x-\frac{π}{3}）$ |