题目内容
12．${∫}_{-π}^{π}$sin2$\frac{x}{2}$dx=（ ）| A． | 0 | B． | π-1 | C． | π | D． | π+1 |
分析 根据定积分的计算法则计算即可
解答 解：${∫}_{-π}^{π}$sin2$\frac{x}{2}$dx=${∫}_{-π}^{π}$$\frac{1}{2}$（1-cosx）dx=$\frac{1}{2}$（x-sinx）|${\;}_{-π}^{π}$=$\frac{1}{2}$（π+π）=π，
故选：C
点评 本题考查了定积分的计算，属于基础题．
练习册系列答案
轻松夺冠全能掌控卷系列答案
相关题目
2．已知数列{an}是等差数列，a2=3，a6=7，则a11的值为（ ）
| A． | 11 | B． | 12 | C． | 13 | D． | 10 |
3．已知-1≤a≤3，2≤b≤4，则2a-b的取值范围是（ ）
| A． | [-6，4] | B． | [0，10] | C． | [-4，2] | D． | [-5，1] |
4．某棱柱的三视图如图示，则该棱柱的体积为（ ）
| A． | 3 | B． | 4 | C． | 6 | D． | 12 |
2．
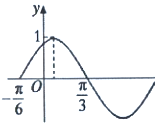函数$f（x）=Asin（{ωx+φ}）（{x∈R，A＞0，ω＞0，|φ|＜\frac{π}{2}}）$的部分图象如图所示，如果${x_1}，{x_2}∈（{-\frac{π}{6}，\frac{π}{3}}）$，且f（x1）=f（x2），则f（x1+x2）=（ ）
函数$f（x）=Asin（{ωx+φ}）（{x∈R，A＞0，ω＞0，|φ|＜\frac{π}{2}}）$的部分图象如图所示，如果${x_1}，{x_2}∈（{-\frac{π}{6}，\frac{π}{3}}）$，且f（x1）=f（x2），则f（x1+x2）=（ ）| A． | $\frac{1}{2}$ | B． | $\frac{{\sqrt{2}}}{2}$ | C． | $\frac{{\sqrt{3}}}{2}$ | D． | 1 |