题目内容
9.在△ABC中,若2cosAcosB=1-cosC,则△ABC是等腰三角形.分析 由三角函数公式化简可得cos(A-B)=1,结合三角形角的范围可得.
解答 解:∵2cosAcosB=1-cosC=1+cos(A+B),
∴2cosAcosB=cosAcosB-sinAsinB+1,
∴cosAcosB+sinAsinB=1,
∴cos(A-B)=1,
∴A-B=0,即A=B,
∴△ABC一定是等腰三角形
故答案是:等腰.
点评 本题考查两角和与差的三角函数,涉及三角形形状的判定,属基础题.

练习册系列答案
相关题目
19.已知三次函数$f(x)=\frac{1}{3}{x^3}-({4m-1}){x^2}+({15{m^2}-2m-7})x+2$在x∈(-∞,+∞)是增函数,则m的取值范围是( )
| A. | m<2或m>4 | B. | -4<m<-2 | C. | 2<m<4 | D. | 以上皆不正确 |
4.某棱柱的三视图如图示,则该棱柱的体积为( )


| A. | 3 | B. | 4 | C. | 6 | D. | 12 |
19.在空间直角坐标系O-xyz中,点(1,2,-2)关于点(-1,0,1)的对称点是( )
| A. | (-3,-2,4) | B. | (3,-2,-4) | C. | (-3,2,-4) | D. | (-3,2,4) |
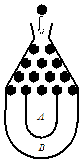 将一个半径适当的小球放入如图所示的容器最上方的入口处,小球将自由下落.小球在下落过程中它将3次遇到黑色障碍物,最后落入A袋或B袋中.已知小球每次遇到黑色障碍物时,向左、右两边下落的概率都是$\frac{1}{2}$.
将一个半径适当的小球放入如图所示的容器最上方的入口处,小球将自由下落.小球在下落过程中它将3次遇到黑色障碍物,最后落入A袋或B袋中.已知小球每次遇到黑色障碍物时,向左、右两边下落的概率都是$\frac{1}{2}$.