题目内容
已知集合A=B=R,x∈A,y∈B,f:x→y=ax+b,若8和14的原像分别是1和3,求5在f作用下的象.
考点:映射
专题:函数的性质及应用
分析:根据映射的定义及条件:8和14的原像分别是1和3,解出a和b,然后再求解;
解答:
解:∵集合A=B=R,x∈A,y∈B,f:x→y=ax+b,
8和14的原像分别是1和3,
∴
,
解得,a=
,b=-
,
∴y=
x-
,
当x=5时,y=
×5-
=0,
即5在f作用下的象为0.
8和14的原像分别是1和3,
∴
|
解得,a=
| 1 |
| 3 |
| 5 |
| 3 |
∴y=
| 1 |
| 3 |
| 5 |
| 3 |
当x=5时,y=
| 1 |
| 3 |
| 5 |
| 3 |
即5在f作用下的象为0.
点评:此题主要考查映射与函数的定义及其应用,理解象与原象的定义,不要弄混淆了,此题是一道好题.

练习册系列答案
相关题目
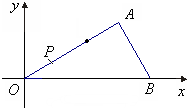 如图,在平面直角坐标系中,△AOB是直角三角形,∠AOB=30°,∠A=90°,OB=12,点P在OA上,且OP=2
如图,在平面直角坐标系中,△AOB是直角三角形,∠AOB=30°,∠A=90°,OB=12,点P在OA上,且OP=2