题目内容
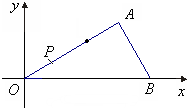 如图,在平面直角坐标系中,△AOB是直角三角形,∠AOB=30°,∠A=90°,OB=12,点P在OA上,且OP=2
如图,在平面直角坐标系中,△AOB是直角三角形,∠AOB=30°,∠A=90°,OB=12,点P在OA上,且OP=2| 3 |
考点:直线的一般式方程
专题:直线与圆
分析:由题意易得P的坐标和AB的斜率,由平行关系可得所求直线的斜率,可得点斜式方程,化为一般式即可.
解答:
解:由题意可得直线OA的斜率为tan30°=
,
由垂直关系可得直线AB的斜率为-
,
设P(a,b),则
,解得
,即P(3,
),
当过P的直线与OB平行时,直线的方程为y=
;
当过P的直线与AB平行时,直线的方程为y-
=-
(x-3),
整理为一般式可得
x+y-4
=0
故答案为:y=
或
x+y-4
=0
| ||
| 3 |
由垂直关系可得直线AB的斜率为-
| 3 |
设P(a,b),则
|
|
| 3 |
当过P的直线与OB平行时,直线的方程为y=
| 3 |
当过P的直线与AB平行时,直线的方程为y-
| 3 |
| 3 |
整理为一般式可得
| 3 |
| 3 |
故答案为:y=
| 3 |
| 3 |
| 3 |
点评:本题考查直线的一般式方程,涉及直线的垂直关系和分类讨论,属基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知a=0.80.7,b=0.80.9,c=1.10.6,则a,b,c的大小关系是( )
| A、b>c>a |
| B、b>a>c |
| C、c>a>b |
| D、a>b>c |
已知
+
+
=
,|
|=2,|
|=3,|
|=
,则向量
与
的夹角为( )
| a |
| b |
| c |
| 0 |
| a |
| b |
| c |
| 7 |
| a |
| b |
| A、30° | B、45° |
| C、60° | D、120° |
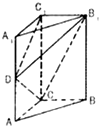 如图,直三棱柱ABC-A1B1C1中AA1=2AC=2BC,D是AA1的中点,CD⊥B1D.
如图,直三棱柱ABC-A1B1C1中AA1=2AC=2BC,D是AA1的中点,CD⊥B1D.