题目内容
计算:7lg20•(
)lg0.7.
| 1 |
| 2 |
考点:对数的运算性质
专题:计算题
分析:设m=7lg20•(
)lg0.7,然后两边取常用对数,利用导数的运算性质化简求得lgm=lg14,从而求得m的值.
| 1 |
| 2 |
解答:
解:设m=7lg20•(
)lg0.7.
两边同取以10为底的对数,得:
lgm=lg{7lg20•(
)lg0.7}
=lg7lg20+lg(
)lg0.7
=lg20×lg7+lg0.7×lg
=(lg10+lg2)×lg7+(lg7-lg10)×(-lg2)
=(1+lg2)×lg7+(lg7-1)×(-lg2)
=lg7+lg7×lg2-lg7×lg2+lg2
=lg7+lg2=lg14.
∴m=14.
即7lg20•(
)lg0.7=14.
| 1 |
| 2 |
两边同取以10为底的对数,得:
lgm=lg{7lg20•(
| 1 |
| 2 |
=lg7lg20+lg(
| 1 |
| 2 |
=lg20×lg7+lg0.7×lg
| 1 |
| 2 |
=(lg10+lg2)×lg7+(lg7-lg10)×(-lg2)
=(1+lg2)×lg7+(lg7-1)×(-lg2)
=lg7+lg7×lg2-lg7×lg2+lg2
=lg7+lg2=lg14.
∴m=14.
即7lg20•(
| 1 |
| 2 |
点评:本题考查了对数的运算性质,体现了数学转化思想方法,是中档题.

练习册系列答案
相关题目
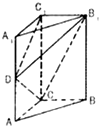 如图,直三棱柱ABC-A1B1C1中AA1=2AC=2BC,D是AA1的中点,CD⊥B1D.
如图,直三棱柱ABC-A1B1C1中AA1=2AC=2BC,D是AA1的中点,CD⊥B1D.