题目内容

求函数f（x）=
x2
x-2
（x≠2）的值域．
考点：函数的值域
专题：计算题,函数的性质及应用
分析：先化简f（x）=
x2
x-2
=（x-2）+
4
x-2
+4，借助基本不等式求值域．
解答： 解：f（x）=
x2
x-2
=（x-2）+
4
x-2
+4，
∵当x-2＞0时，（x-2）+
4
x-2
≥4，
∴当x-2＜0时，（x-2）+
4
x-2
≤-4，
∴（x-2）+
4
x-2
+4≥8或≤0，
则函数f（x）=
x2
x-2
（x≠2）的值域为（-∞，0]∪[8，+∞）．
点评：本题考查了利用基本不等式求函数的值域，属于基础题．
练习册系列答案
相关题目
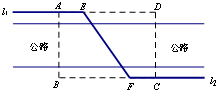如图，某自来水公司要在公路两侧铺设水管，公路为东西方向，在路北侧沿直线铺设线路l1，在路南侧沿直线铺设线路l2，现要在矩形区域ABCD内沿直线将l1与l2接通．已知AB=60m，BC=80m，公路两侧铺设水管的费用为每米1万元，穿过公路的EF部分铺设水管的费用为每米2万元，设∠EFB=
π
2
-α，矩形区域内的铺设水管的总费用为W．
（1）求W关于α的函数关系式；
（2）求W的最小值及相应的角α．
已知函数f（x）=|x|（a-x），a∈R．
（1）若函数f（x）在x∈[0，2]上是单调函数，求实数a的取值范围．
（2）对于确定的正数b，不等式|x|（a-x）≤b，对x∈[-1，2]恒成立，求实数a的取值范围．
以下是关于函数f（x）=
4|x|
x2+1
的四个命题：
①f（x）的图象关于y轴对称；
②f（x）在区间[-1，0]∪[1，+∞）上单调递减；
③f（x）在x=-1处取得极小值，在x=1处取得极大值；
④f（x）有最大值，无最小值；
⑤若方程f（x）-k=0至少有三个不同的实根，则实数k的取值范围是（0，2）．
其中为真命题的是
 
（请填写你认为是真命题的序号）．
y=
a
|a|
+
b
|b|
+
c
|c|
+
abc
|abc|
，求y的范围
 
．
在△ABC中，B=45°，A=75°，c=1，则最短边的边长为（　　）
A、
6
2
B、1
C、
3
2
+
6
12
D、
6
3
已知α为第二象限角，且tan（π-α）-3=0，则cosα的值为
 
．
已知函数f（x）是定义在R上的偶函数，且当x≤0时，f（x）=x2+2x．
（1）现已画出函数f（x）在y轴左侧的图象，如图所示，请补出完整函数f（x）的图象，并根据图象写出函数f（x）的增区间；
（2）写出函数f（x）的解析式和值域．
（3）若F（x）=f（x）-f（-x），试判断F（x）的奇偶性，并证明你的结论．
（1-x+x2）3（1-2x）3=a0+a1x+a2x2+…+a9x9，则a0+a2+a4+…+a8=（　　）
A、364B、-415
C、415D、-364

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网