题目内容
16.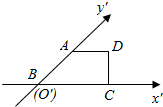 有一块多边形的菜地,它的水平放置的平面图形的斜二测直观图是直角梯形(如图)∠ABC=45°,AB=$\sqrt{2}$,AD=1,DC⊥BC,则这块菜地的面积为$3\sqrt{2}$.
有一块多边形的菜地,它的水平放置的平面图形的斜二测直观图是直角梯形(如图)∠ABC=45°,AB=$\sqrt{2}$,AD=1,DC⊥BC,则这块菜地的面积为$3\sqrt{2}$.
分析 以O点为坐标原点,在直观图中建立平面直角坐标系,按斜二测画直观图的原则,找到四边形ABCD的四个顶点在平面直角坐标系下对应的点,即把直观图中的点还原回原图形中,连结后得到原图形,然后利用梯形面积公式求解.
解答  解:如图,
解:如图,
直观图四边形的边BC在x′轴上,在原坐标系下在x轴上,长度不变,
点A在y′轴上,在原图形中在y轴上,且BE长度为AB长的2倍,过E作EF∥x轴,
且使EF长度等于AD,则点F为点D在原图形中对应的点.
∴四边形EBCF为四边形ABCD的原图形.
在直角梯形ABCD中,由AB=$\sqrt{2}$,AD=1,得BC=2.
∴四边形EBCF的面积S=$\frac{1}{2}$(EF+BC)•BE=$\frac{1}{2}$(1+2)×2$\sqrt{2}$=$3\sqrt{2}$,
故答案为:$3\sqrt{2}$.
点评 本题考查了水平放置的平面图形的直观图的画法,考查了原图形和直观图面积之间的关系,难度不大,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.椭圆3x2+2y2=6的焦距为( )
| A. | 1 | B. | 2 | C. | $\sqrt{5}$ | D. | $2\sqrt{5}$ |
4.复数z=$\frac{2}{1-i}$,则复数z的模是( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2$\sqrt{2}$ |
1.某几何体的三视图如图所示,则该几何体的体积是( )
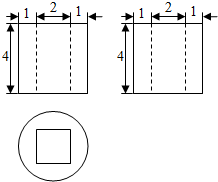

| A. | 16π-16 | B. | 16π | C. | 16π-8 | D. | 64 |
6.方程lgx+x=0的根所在的区间是( )
| A. | $(0,\frac{1}{4})$ | B. | $(\frac{1}{4},\frac{1}{2})$ | C. | $(\frac{1}{2},\frac{3}{4})$ | D. | $(\frac{3}{4},1)$ |
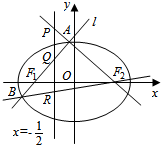 设F1,F2分别是椭圆C:$\frac{{x}^{2}}{2}$+y2=1的左、右焦点,过F1且斜率不为零的动直线l与椭圆C交于A,B两点.
设F1,F2分别是椭圆C:$\frac{{x}^{2}}{2}$+y2=1的左、右焦点,过F1且斜率不为零的动直线l与椭圆C交于A,B两点.