题目内容
已知数列{an}满足:a1=-
,an=1-
(n>1),则a1•a2•…•a2013= .
| 1 |
| 4 |
| 1 |
| an-1 |
考点:数列的概念及简单表示法
专题:计算题,等差数列与等比数列
分析:确定数列{an}是以3为周期的周期数列,且a1•a2•a3=-1,即可求出a1•a2•…•a2013.
解答:
解:∵数列{an}满足:a1=-
,an=1-
(n>1),
∴a2=5,a3=
,a4=-
,
∴数列{an}是以3为周期的周期数列,且a1•a2•a3=-1,
∴a1•a2•…•a2013=-1.
故答案为:-1.
| 1 |
| 4 |
| 1 |
| an-1 |
∴a2=5,a3=
| 4 |
| 5 |
| 1 |
| 4 |
∴数列{an}是以3为周期的周期数列,且a1•a2•a3=-1,
∴a1•a2•…•a2013=-1.
故答案为:-1.
点评:本题考查数列的通项,确定数列{an}是以3为周期的周期数列是关键.

练习册系列答案
相关题目
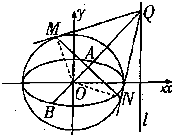 如图,已知椭圆
如图,已知椭圆 如图,为了测量点A与河流对岸点B之间的距离,在点A同侧选取点C,若测得AC=40米,∠BAC=75°,∠ACB=60°,则点A与点B之间的距离等于
如图,为了测量点A与河流对岸点B之间的距离,在点A同侧选取点C,若测得AC=40米,∠BAC=75°,∠ACB=60°,则点A与点B之间的距离等于