题目内容
19.在二项式${(\frac{1}{2x}+2x)^n}$的展开式中,第一、二项及最后两项的二项式系数之和共为18,则展开式中x4的系数为448.(用数字作答)分析 由题意利用二项式系数的性质求得n=8,再根据二项展开式的通项公式求得展开式中x4的系数.
解答 解:∵第一、二项及最后两项的二项式系数之和共为18,
∴Cn0+Cn1+Cnn-1+Cnn=18,
解得n=8,
∴二项式${(\frac{1}{2x}+2x)^n}$的展开式的通项为C8r22r-8x2r-8,
令2r-8=4,
解得r=6,
∴展开式中x4的系数为C8624=448,
故答案为:448.
点评 本题主要考查二项式定理的应用,二项展开式的通项公式,二项式系数的性质,属于基础题.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
10.执行如图所示的程序框图,如果输出的结果为0,那么输入的x为( )


| A. | $\frac{1}{9}$ | B. | -1或1 | C. | 1 | D. | -1 |
14.已知x>0,y>0,$\frac{2}{x}+\frac{1}{y}=\frac{1}{3}$,x+2y>m2-2m恒成立,则m的取值范围是( )
| A. | [-6,4] | B. | [-4,6] | C. | (-4,6) | D. | (-6,4) |
8.按如图所示的程序框图,若输入a=81,则输出的i=( )
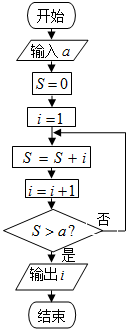

| A. | 14 | B. | 17 | C. | 19 | D. | 21 |
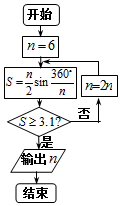 公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术”.利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出n的值为(参考数据:sin15°=0.2588,sin7.5°=0.1305)( )
公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术”.利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出n的值为(参考数据:sin15°=0.2588,sin7.5°=0.1305)( ) 如图所示,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的焦距为2,直线y=x被椭圆C截得的弦长为$\frac{4\sqrt{3}}{3}$.
如图所示,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的焦距为2,直线y=x被椭圆C截得的弦长为$\frac{4\sqrt{3}}{3}$.