题目内容
若方程sin2x+sinx-1-a=0在(0,
)上有解,则a的取值范围 .
| π |
| 2 |
考点:函数的零点
专题:函数的性质及应用
分析:由x的范围得到sinx的范围,把方程转化为t2+t-1=a,令f(t)=t2+t-1求出其值域得答案.
解答:
解:设t=sinx,
∵x∈(0,
),则t∈(0,1),
即方程sin2x+sinx-1-a=0化为t2+t-1=a,
方程sin2x+sinx-1-a=0在(0,
)上有解,
即t2+t-1=a在(0,1)上有解.
令f(t)=t2+t-1,则f(t)=t2+t-1=(t+
)2-
∈(-1,1),
则a的取值范围是(-1,1).
故答案为:(-1,1).
∵x∈(0,
| π |
| 2 |
即方程sin2x+sinx-1-a=0化为t2+t-1=a,
方程sin2x+sinx-1-a=0在(0,
| π |
| 2 |
即t2+t-1=a在(0,1)上有解.
令f(t)=t2+t-1,则f(t)=t2+t-1=(t+
| 1 |
| 2 |
| 5 |
| 4 |
则a的取值范围是(-1,1).
故答案为:(-1,1).
点评:本题考查了函数的零点,考查了数学转化思想方法,是基础题.

练习册系列答案
相关题目
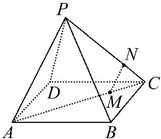 如图,四棱锥P-ABCD中,M,N分别为AC,PC上的点,且MN∥平面PAD,则( )
如图,四棱锥P-ABCD中,M,N分别为AC,PC上的点,且MN∥平面PAD,则( )| A、MN∥PD |
| B、MN∥PA |
| C、MN∥AD |
| D、以上均有可能 |
函数f(x)=sinx+cos2x的图象为( )
A、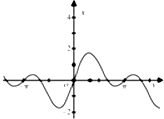 |
B、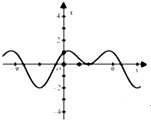 |
C、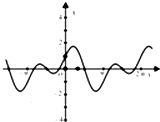 |
D、 |