Question

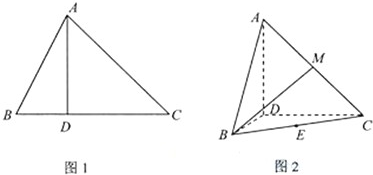
如图1，∠ACB=45°，BC=4，过动点A作AD⊥BC，垂足D在线段BC上且异于点B，连接AB，沿AD将△ABD折起，使∠BDC=90°（如图2所示）

（1）当BD的长为多少时，△BCD的体积最大；
（2）当△BCD的体积最大时，设点M为棱AC的中点，试求直线BM与CD所成角的正弦值．

Answer 1

考点：棱柱、棱锥、棱台的体积,异面直线及其所成的角

专题：计算题,空间位置关系与距离,空间角

分析：（1）设BD=x，先利用线面垂直的判定定理证明AD即为三棱锥A-BCD的高，再将三棱锥的体积表示为x的函数，最后利用导数求函数的最大值即可；
（2）以D为原点，建立空间直角坐标系D-xyz，三棱锥A-BCD的体积最大时，BD=

4

3

，AD=CD=

8

3

，确定

BM

=（-

4

3

，

4

3

，

4

3

），

DC

=（0，

8

3

，0），利用向量的夹角公式，即可求直线BM与CD所成角的正弦值．

解答： 解：（1）设BD=x，则CD=4-x
∵∠ACB=45°，AD⊥BC，∴AD=CD=4-x
∵折起前AD⊥BC，∴折起后AD⊥BD，AD⊥CD，BD∩DC=D
∴AD⊥平面BCD
∴V_A-BCD=

1

3

×AD×S_△BCD=

1

3

×（4-x）×

1

2

×x（4-x）=

1

6

（x³-8x²+16x）
设f（x）=

1

6

（x³-8x²+16x），x∈（0，4），
∵f′（x）=

1

6

（x-4）（3x-4），∴f（x）在（0，

4

3

）上为增函数，在（

4

3

，4）上为减函数
∴当x=

4

3

时，函数f（x）取最大值
∴当BD=

4

3

时，三棱锥A-BCD的体积最大；
（2））∵∠BDC=90°，∴DB，DC，DA两两垂直，以D为原点，建立空间直角坐标系D-xyz，
三棱锥A-BCD的体积最大时，BD=

4

3

，AD=CD=

8

3

∴D（0，0，0），B（

4

3

，0，0），C（0，

8

3

，0），M（0，

4

3

，

4

3

），
设直线BM与CD所成角为θ，则

BM

=（-

4

3

，

4

3

，

4

3

），

DC

=（0，

8

3

，0），
∴cosθ=

32 9

4 3 3 • 8 3

=

3

3

∴直线BM与CD所成角的正弦值为

6

3

．

点评：本题主要考查了线面垂直的判定，折叠问题中的不变量，空间线面角的计算方法，空间向量、空间直角坐标系的运用，有一定的运算量，属中档题．