题目内容
若2cos2α=sin(α+
),则sin2α的值为 .
| π |
| 4 |
考点:二倍角的余弦
专题:三角函数的求值
分析:由条件利用两角和的正弦公式、二倍角公式求得,cosα-sinα,或 cosα+sinα的值,由此求得sin2α的值.
解答:
解:∵2cos2α=sin(
+α),
∴2(cos2α-sin2α)=
(sinα+cosα),
∴cosα-sinα=
,或cosα+sinα=0.
当cosα-sinα=
,则有1-sin2α=
,sin2α=
;
当cosα+sinα=0时,两边平方可解得:sin2α=-1,
故答案为:-1或
.
| π |
| 4 |
∴2(cos2α-sin2α)=
| ||
| 2 |
∴cosα-sinα=
| ||
| 4 |
当cosα-sinα=
| ||
| 4 |
| 1 |
| 8 |
| 7 |
| 8 |
当cosα+sinα=0时,两边平方可解得:sin2α=-1,
故答案为:-1或
| 7 |
| 8 |
点评:本题主要考查两角和差的正弦、余弦公式的应用,二倍角公式的应用,属于中档题.

练习册系列答案
相关题目
从4个不同的树种里选出3个品种,分别种植在三条不同的道路旁,不同的种植方法种数为( )
| A、4 | B、12 | C、24 | D、72 |
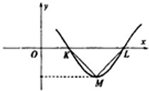 设偶函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,△KLM为等腰直角三角形,∠KML=90°,|KL|=1,则f(
设偶函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,△KLM为等腰直角三角形,∠KML=90°,|KL|=1,则f(| 1 |
| 3 |
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|
二项式(
-x
)n展开式中含有常数项,则n可能的取值是( )
| 1 |
| x |
| x |
| A、8 | B、7 | C、6 | D、5 |
已知a∈R,则“a>2”是“a2>2|a|”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |