Question

已知f（x）是有y=log₂x的反函数，又g（x）=-2x+b，且f（x）与g（x）的交点为M（m，n）．
（1）判定g（x）的单调性；
（2）若m=1，定义min（a，b）=

a，(a≤b) b，(a＞b)

，记F（x）=min{f（x），g（x）}，求其解析式及最大值．

Answer 1

考点：反函数,函数解析式的求解及常用方法

专题：函数的性质及应用

分析：（1）由-2＜0，可得g（x）=-2x+b为R上的单调递减函数．
（2）由f（x）是有y=log₂x的反函数，可得f（x）=2^x（x∈R）．由f（x）与g（x）的交点为M（m，n）．可得

n=-2+b n=2

，解得n=2，b=4．可得f（x）=2^x，g（x）=-2x+4．F（x）=min{f（x），g（x）}=

f(x)，x≤2 g(x)，x＞2

．

解答： 解：（1）∵-2＜0，∴g（x）=-2x+b为R上的单调递减函数．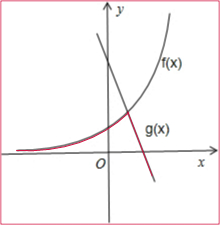
（2）∵f（x）是y=log₂x的反函数，∴f（x）=2^x（x∈R）．
联立

y=-2x+b y=2x

，即

n=-2+b n=2

，解得n=2，b=4．
∴f（x）=2^x，g（x）=-2x+4．
F（x）=min{f（x），g（x）}=

f(x)，x≤2 g(x)，x＞2

=

2x，x≤2 -2x+4，x＞2

，
函数F（x）的最大值为F（1）=2．

点评：本题考查了反函数的求法、一次函数的单调性、“取小函数”，考查了推理能力与数形结合的思想方法，考查了计算能力，属于基础题．