题目内容
求下列函数的值域:y=
.
| cosx+2 |
| sinx-1 |
考点:函数的值域
专题:计算题,作图题,函数的性质及应用
分析:y=
的几何意义是点A(1,-2)与点B(sinx,cosx)连线的斜率,作图象求解.
| cosx+2 |
| sinx-1 |
解答:
解:y=
的几何意义是点A(1,-2)与点B(sinx,cosx)连线的斜率,
作图象如下,
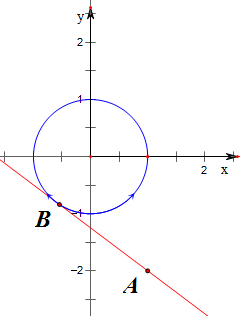
设直线AB的方程为y=k(x-1)-2;
化简可得,kx-y-k-2=0,
则
=1;
解得,k=-
;
结合图象可得,
k≤-
;
故函数的值域为(-∞,-
].
| cosx+2 |
| sinx-1 |
作图象如下,

设直线AB的方程为y=k(x-1)-2;
化简可得,kx-y-k-2=0,
则
| |k+2| | ||
|
解得,k=-
| 3 |
| 4 |
结合图象可得,
k≤-
| 3 |
| 4 |
故函数的值域为(-∞,-
| 3 |
| 4 |
点评:本题考查了函数值域的求法.高中函数值域求法有:1、观察法,2、配方法,3、反函数法,4、判别式法;5、换元法,6、数形结合法,7、不等式法,8、分离常数法,9、单调性法,10、利用导数求函数的值域,11、最值法,12、构造法,13、比例法.要根据题意选择.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
已知命题p:π是无理数;命题q:π是有理数;则以下命题中的假命题是( )
| A、p或q | B、p且¬q |
| C、¬p或¬q | D、¬p且q |
函数f(x)=min(2
,|x-2|},其中min(a,b)=
,若动直线y=m与函数y=f(x)的图象有三个不同的交点,它们的横坐标分别为x1,x2,x3,则x1x2x3的最大值( )
| x |
|
| A、2 | B、3 | C、1 | D、不存在 |
将函数y=
-
(x∈[0,2])的图象绕坐标原点逆时针旋转θ(θ为锐角),若所得曲线仍是一个函数的图象,则θ的范围是( )
| -x2+2x+3 |
| 3 |
A、(0,
| ||||
B、(0,
| ||||
C、(
| ||||
D、[
|