题目内容
在实数集R中定义一种运算“*”,对任意a,b∈R,a*b为唯一确定的实数,且具有性质:
(1)对任意a∈R,a*0=a;
(2)对任意a,b,c∈R,(a*b)*c=(ab)*c+(a*c)+(b*c)-2c.
如:3*2=(3*2)*0=(3×2)*0+(3*0)+(2*0)-2×0=6+3+2-0=11.
关于函数f(x)=(2x)*
的性质,有如下说法:
①函数f(x)的最小值为3;
②函数f(x)的图象关于点(0,1)成中心对称;
③函数f(x)为奇函数;
④函数f(x)的单调递增区间为(-∞,-
), &(
,+∞).
其中所有正确说法的个数为( )
(1)对任意a∈R,a*0=a;
(2)对任意a,b,c∈R,(a*b)*c=(ab)*c+(a*c)+(b*c)-2c.
如:3*2=(3*2)*0=(3×2)*0+(3*0)+(2*0)-2×0=6+3+2-0=11.
关于函数f(x)=(2x)*
| 1 |
| 2x |
①函数f(x)的最小值为3;
②函数f(x)的图象关于点(0,1)成中心对称;
③函数f(x)为奇函数;
④函数f(x)的单调递增区间为(-∞,-
| 1 |
| 2 |
| 1 |
| 2 |
其中所有正确说法的个数为( )
| A、0 | B、1 | C、2 | D、3 |
考点:函数奇偶性的判断,命题的真假判断与应用,函数单调性的判断与证明
专题:新定义,函数的性质及应用
分析:由新定义可得:函数f(x)=1+2x+
.
①利用基本不等式即可判断出;
②判断f(-x)+f(x)=2是否成立;
③判断f(-x)+f(x)=0是否成立;
④利用导数解出f′(x)>0即可.
| 1 |
| 2x |
①利用基本不等式即可判断出;
②判断f(-x)+f(x)=2是否成立;
③判断f(-x)+f(x)=0是否成立;
④利用导数解出f′(x)>0即可.
解答:
解:由新定义可得:函数f(x)=(2x)*
=(2x*
)*0
=(2x•
)*0+(2x*0)+(
*0)-2×0
=1+2x+
.
据此可得:
①当x>0时,f(x)≥1+2
=3,当且仅当x=
时取等号;同理可得:当x<0时,f(x)≤1-2=-1.
∴①不正确;
②∵f(-x)+f(x)=1-2x+
+1+2x+
=2,
∴函数f(x)的图象关于点(0,1)成中心对称,因此正确;
③由②可知:f(-x)+f(x)≠0,可知:
函数f(x)不是奇函数,因此不正确;
④由f′(x)=2-
=
>0,解得x>
或x<-
.
∴函数f(x)的单调递增区间为(-∞,-
),(
,+∞),因此④正确.
综上可知:只有②④正确.
故选:C.
| 1 |
| 2x |
=(2x*
| 1 |
| 2x |
=(2x•
| 1 |
| 2x |
| 1 |
| 2x |
=1+2x+
| 1 |
| 2x |
据此可得:
①当x>0时,f(x)≥1+2
2x•
|
| 1 |
| 2 |
∴①不正确;
②∵f(-x)+f(x)=1-2x+
| 1 |
| -2x |
| 1 |
| 2x |
∴函数f(x)的图象关于点(0,1)成中心对称,因此正确;
③由②可知:f(-x)+f(x)≠0,可知:
函数f(x)不是奇函数,因此不正确;
④由f′(x)=2-
| 1 |
| 2x2 |
2(x+
| ||||
| 2x2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴函数f(x)的单调递增区间为(-∞,-
| 1 |
| 2 |
| 1 |
| 2 |
综上可知:只有②④正确.
故选:C.
点评:本题综合考查了新定义、函数的单调性、奇偶性、对称性、基本不等式等基础知识与基本技能方法,考查了解决新问题的能力,属于难题.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
设变量x,y满足约束条件
.目标函数z=x+2y,则z的取值范围为( )
|
| A、[1,2] |
| B、[1,11] |
| C、[2,11] |
| D、[0,11] |
函数f(x)=sin2x-sin(2x+
)的最小值为( )
| π |
| 3 |
| A、0 | ||
| B、-1 | ||
C、-
| ||
| D、-2 |
已知实数x,y满足约束条件
,则z=2y-x的最小值是( )
|
| A、-1 | ||
| B、0 | ||
| C、1 | ||
D、
|
在下列四个命题中
①y=1是幂函数;
②“x<1”是“x<2”的充分不必要条件;
③命题“存在x∈R,x2-2>0”的否定是:“任意x∈R,x2-x<0”
④若a=-1,则函数f(x)=ax2+2x-1只有一个零点.
其中错误的个数有( )个.
①y=1是幂函数;
②“x<1”是“x<2”的充分不必要条件;
③命题“存在x∈R,x2-2>0”的否定是:“任意x∈R,x2-x<0”
④若a=-1,则函数f(x)=ax2+2x-1只有一个零点.
其中错误的个数有( )个.
| A、4 | B、2 | C、3 | D、1 |
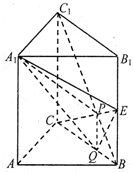 如图在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AA1=2,E是BB1的中点,且CE交BC1于点P,点Q在线段BC上,CQ=2QB.
如图在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AA1=2,E是BB1的中点,且CE交BC1于点P,点Q在线段BC上,CQ=2QB.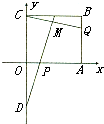 如图所示,在直角坐标平面上的矩形OABC中,|OA|=2,|OC|=
如图所示,在直角坐标平面上的矩形OABC中,|OA|=2,|OC|=