题目内容
直角坐标的坐标原点与极坐标的极点重合,x轴正半轴为极轴,长度单位相同.若直线l方程
(t为参数),圆C方程为ρ=2COSθ,ρ与⊙C相交于A、B两点.
(Ⅰ)写出直线l的极坐标方程(不必化简);
(Ⅱ)求弦长|AB|.
|
(Ⅰ)写出直线l的极坐标方程(不必化简);
(Ⅱ)求弦长|AB|.
考点:简单曲线的极坐标方程,参数方程化成普通方程
专题:坐标系和参数方程
分析:(I)由直线l方程
(t为参数),可得t=x+1,代入y=2t-3即可得出直角坐标方程.把
代入即可得出极坐标方程.
(2)由圆C方程为ρ=2cosθ,化为ρ2=2ρcosθ,可得(x-1)2+y2=1,可得圆心C(1,0),半径r=1.利用点到直线的距离公式可得圆心C到直线l的距离d,再利用弦长|AB|=2
即可得出.
|
|
(2)由圆C方程为ρ=2cosθ,化为ρ2=2ρcosθ,可得(x-1)2+y2=1,可得圆心C(1,0),半径r=1.利用点到直线的距离公式可得圆心C到直线l的距离d,再利用弦长|AB|=2
| r2-d2 |
解答:
解:(I)∵直线l方程
(t为参数),∴直角坐标方程为y=2x-1,
把
代入可得ρsinθ=2ρcosθ-1.
(2)由圆C方程为ρ=2cosθ,化为ρ2=2ρcosθ,∴x2+y2=2x,即(x-1)2+y2=1,可得圆心C(1,0),半径r=1.
∴圆心C到直线l的距离d=
=
.
∴弦长|AB|=2
=2
=
.
|
把
|
(2)由圆C方程为ρ=2cosθ,化为ρ2=2ρcosθ,∴x2+y2=2x,即(x-1)2+y2=1,可得圆心C(1,0),半径r=1.
∴圆心C到直线l的距离d=
| |2-1| | ||
|
| 1 | ||
|
∴弦长|AB|=2
| r2-d2 |
1-
|
4
| ||
| 5 |
点评:本题考查了极坐标方程参数方程化为普通方程、点到直线的距离公式、弦长|AB|=2
,考查了计算能力,属于基础题.
| r2-d2 |

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
若非直角△ABC的内角A、B、C成等差数列,则tanA+tanC-tanAtanBtanC=( )
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|
设a=log23,b=log2
,c=(
)1.2,则它们的大小关系是( )
| 1 |
| 3 |
| 1 |
| 2 |
| A、c<a<b |
| B、b<c<a |
| C、b<a<c |
| D、c<b<a |
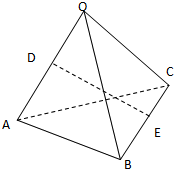 如图,空间四边形OABC各边以及AC,BO的长都是1,点D是边OA,BC的中点,连接DE.
如图,空间四边形OABC各边以及AC,BO的长都是1,点D是边OA,BC的中点,连接DE.