题目内容
已知
=(
sinωx,-cosωx),
=(cosωx,cosωx),ω>0,函数f(x)=
•
,且f(x)的图象相邻两条对称轴间的距离为
.
(Ⅰ)求函数f(x)的最小正周期和单调增区间;
(Ⅱ)已知△ABC的内角A,B,C所对的边分别为a,b,c,若a=
,b=2,且f(
)=
,求△ABC的面积.
| a |
| 3 |
| b |
| a |
| b |
| π |
| 2 |
(Ⅰ)求函数f(x)的最小正周期和单调增区间;
(Ⅱ)已知△ABC的内角A,B,C所对的边分别为a,b,c,若a=
| 7 |
| A |
| 2 |
| 1 |
| 2 |
考点:余弦定理,两角和与差的正弦函数,三角函数的周期性及其求法
专题:解三角形
分析:(Ⅰ)由两向量的坐标,利用平面向量的数量积运算法则列出f(x)解析式,整理后根据相邻两条对称轴间的距离求出最小正周期,利用周期公式求出ω的值,确定出f(x)解析式,利用正弦函数的单调性求出f(x)的单调增区间即可;
(Ⅱ)由f(
)=
,确定出A的度数,再由a,b的值,利用余弦定理求出c的值,根据三角形面积公式求出三角形ABC面积即可.
(Ⅱ)由f(
| A |
| 2 |
| 1 |
| 2 |
解答:
解:(Ⅰ)∵
=(
sinωx,-cosωx),
=(cosωx,cosωx),ω>0
∴f(x)=
•
=
sinωxcosωx-cosωxcosωx=
sin2ωx-
cos2ωx-
=sin(2ωx-
)-
,
∵f(x)相邻两条对称轴的距离为
,∴f(x)最小正周期为π,
由
=π,得ω=1,即函数f(x)=sin(2x-
)-
,
由2kπ-
≤2x-
≤2kπ+
,k∈Z,得kπ-
≤x≤kπ+
,k∈Z,
∴函数f(x)的单调增区间[kπ-
,kπ+
],k∈Z;
(Ⅱ)∵f(
)=sin(A-
)-
=
,
∴sin(A-
)=1,
∵0<A<π,∴-
<A-
<
,
∴A=
,
在△ABC中,a=
,b=2,
由余弦定理得a2=b2+c2-2bccosA,即7=4+c2+2c,
解得:c=3或c=-1(舍去),
则S△ABC=
bcsinA=
.
| a |
| 3 |
| b |
∴f(x)=
| a |
| b |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 6 |
| 1 |
| 2 |
∵f(x)相邻两条对称轴的距离为
| π |
| 2 |
由
| 2π |
| 2ω |
| π |
| 6 |
| 1 |
| 2 |
由2kπ-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
| π |
| 3 |
∴函数f(x)的单调增区间[kπ-
| π |
| 6 |
| π |
| 3 |
(Ⅱ)∵f(
| A |
| 2 |
| π |
| 6 |
| 1 |
| 2 |
| 1 |
| 2 |
∴sin(A-
| π |
| 6 |
∵0<A<π,∴-
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
∴A=
| 2π |
| 3 |
在△ABC中,a=
| 7 |
由余弦定理得a2=b2+c2-2bccosA,即7=4+c2+2c,
解得:c=3或c=-1(舍去),
则S△ABC=
| 1 |
| 2 |
3
| ||
| 2 |
点评:此题考查了余弦定理,平面向量的数量积运算,正弦函数的单调性,以及三角形面积公式,熟练掌握余弦定理是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若非直角△ABC的内角A、B、C成等差数列,则tanA+tanC-tanAtanBtanC=( )
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|
函数f(x)=2x-
为偶函数,则下列函数中在区间(0,2)上递减的是( )
| a |
| 2x |
| A、f(x)=x2+2ax-1 | ||
| B、f(x)=(1-a)x | ||
| C、f(x)=-ax3-12x+1 | ||
D、f(x)=x-
|
设偶函数f(x)的定义域为R,当x∈[0,+∞)时,f(x)是减函数,则f(-2),f(π),f(-1)的大小关系是( )
| A、f(-2)<f(-1)<f(π) |
| B、f(-2)<f(π)<f(-1) |
| C、f(-2)>f(π)>f(-1) |
| D、f(-1)>f(-2)>f(π) |
设a=log23,b=log2
,c=(
)1.2,则它们的大小关系是( )
| 1 |
| 3 |
| 1 |
| 2 |
| A、c<a<b |
| B、b<c<a |
| C、b<a<c |
| D、c<b<a |
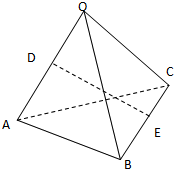 如图,空间四边形OABC各边以及AC,BO的长都是1,点D是边OA,BC的中点,连接DE.
如图,空间四边形OABC各边以及AC,BO的长都是1,点D是边OA,BC的中点,连接DE.