题目内容
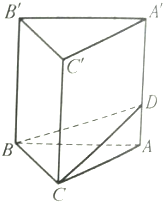 已知正三棱柱的底面边长是4厘米,过BC的一个平面与底面成30°的二面角,交侧棱AA′于D,求AD的长和截面△BCD的面积.
已知正三棱柱的底面边长是4厘米,过BC的一个平面与底面成30°的二面角,交侧棱AA′于D,求AD的长和截面△BCD的面积.考点:点、线、面间的距离计算
专题:空间位置关系与距离,空间角
分析:首先做出二面角的平面角,进一步利用面面间的关系求出AD的长和三角形的面积.
解答:
 解:取BC的中点E,连接AE和DE,
解:取BC的中点E,连接AE和DE,
则:AA1⊥平面ABC,
得到:AA1⊥BC
由于:AE⊥BC
所以:DE⊥BC
所以:∠DAE是平面ABC和DBC所成的二面角的平面角.
则:利用解三角形知识:tan30°=
解得:AD=2
S△BCD=
•BC•DE=
•4•4=8
故答案为:AD=2,S△BCD=8
 解:取BC的中点E,连接AE和DE,
解:取BC的中点E,连接AE和DE,则:AA1⊥平面ABC,
得到:AA1⊥BC
由于:AE⊥BC
所以:DE⊥BC
所以:∠DAE是平面ABC和DBC所成的二面角的平面角.
则:利用解三角形知识:tan30°=
| AD |
| AE |
解得:AD=2
S△BCD=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:AD=2,S△BCD=8
点评:本题考查的知识要点:二面角的应用,解直角三角形,三角形面积的应用.属于基础题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知角θ的顶点与原点重合,始边与x轴正半轴重合,终边在直线y=2x上,则sin(2θ+
)的值为( )
| π |
| 4 |
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
下列函数中,与函数y=
定义域相同的函数为( )
| 1 | ||
|
A、y=
| ||
B、y=
| ||
| C、y=x-2 | ||
| D、y=lnx |
以双曲线y2-x2=2的一个焦点为圆心,离心率为半径的圆的方程是( )
| A、x2+(y±2)2=2 |
| B、(x±2)2+y2=2 |
| C、x2+(y±2)2=4 |
| D、(x±2)2+y2=4 |
一艘海轮从A处出发,以每小时60海里的速度沿东偏南50°方向直线航行,30分钟后到达B处,在C处有一座灯塔,海轮在A处观察灯塔,其方向是东偏南20°,在B处观察灯塔,其方向是北偏东65°,那么B、C两点间的距离是( )
A、10
| ||
B、10
| ||
C、15
| ||
D、20
|
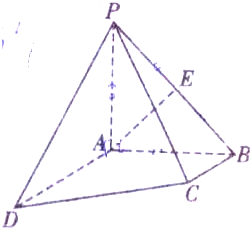 如图,四棱锥P-ABCD中,底面是ABCD是梯形,AD∥BC,AD>BC,∠BAD=90°,PA⊥底面ABCD,PA=AB,点E是PB的中点
如图,四棱锥P-ABCD中,底面是ABCD是梯形,AD∥BC,AD>BC,∠BAD=90°,PA⊥底面ABCD,PA=AB,点E是PB的中点