题目内容
以椭圆9x2+16y2=144的顶点为焦点,且过椭圆焦点的双曲线方程是 .
考点:椭圆的简单性质,双曲线的标准方程
专题:圆锥曲线的定义、性质与方程
分析:由椭圆9x2+16y2=144化为
+
=1,顶点为(4,0),(-4,0),焦点为(±
,0).即可得出双曲线的焦点与顶点,得出双曲线的方程.
| x2 |
| 16 |
| y2 |
| 9 |
| 7 |
解答:
解:椭圆9x2+16y2=144化为
+
=1,顶点为(4,0),(-4,0).
焦点为(±
,0).
∴双曲线的焦点为(4,0),(-4,0),顶点为(±
,0).
∴a=
,c=4,b2=c2-a2=9.
∴双曲线方程为
-
=1.
故答案为:
-
=1.
| x2 |
| 16 |
| y2 |
| 9 |
焦点为(±
| 7 |
∴双曲线的焦点为(4,0),(-4,0),顶点为(±
| 7 |
∴a=
| 7 |
∴双曲线方程为
| x2 |
| 7 |
| y2 |
| 9 |
故答案为:
| x2 |
| 7 |
| y2 |
| 9 |
点评:本题考查了椭圆与双曲线的标准方程及其性质,属于基础题.

练习册系列答案
相关题目
 在如表所示的5×5正方形的25个空格中填入正整数,使得每一行、每列都成等差数列,问必须填进标有*号的空格的数是
在如表所示的5×5正方形的25个空格中填入正整数,使得每一行、每列都成等差数列,问必须填进标有*号的空格的数是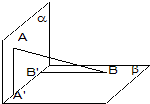 如图,平面α⊥平面β,A∈α,B∈β,AB与两平面α、β所成的角分别为45°和30°,过A、B分别作两平面交线的垂线,垂足为A′、B′,则AB:A′B′=
如图,平面α⊥平面β,A∈α,B∈β,AB与两平面α、β所成的角分别为45°和30°,过A、B分别作两平面交线的垂线,垂足为A′、B′,则AB:A′B′=