题目内容
在如表所示的5×5正方形的25个空格中填入正整数，使得每一行、每列都成等差数列，问必须填进标有*号的空格的数是考点：等差数列的通项公式
专题：等差数列与等比数列
分析：利用等差数列的性质可求得第三行第三列的数，它也是第三行第一列与第五列的等差数列，从而可得x，y的关系式，同理可得第四行第二列的数是第四行第一列与第三列的等差中项，再从纵向中得到相应关系，从而可求得x，y的值．
解答：
解：由题意，第三行第三列的数为206-2x，
所以2（206-2x）=2y+186，所以2x+y=113，①
又第四行第二列的数为74+
×2，
∴y+103=2（74+
×2），
∴4x-3y=161②
由①②解得：x=50，y=13．
∴设第一列等差数列的首项为a1，公差为d，则d=0-y=-13，
∴0=a1+4d，
∴a1=52，即第一行第一列的数为52；
在第三列中，其公差d′=2x-103=100-103=-3，
∴第三列的首项为b1=b5-4d′=100-4×（-3）=112；
∵第一行中的数成等差数列，第一项a1=52，第三项为112，
∴第四项※=52+3×
=142．
故答案为：142．
所以2（206-2x）=2y+186，所以2x+y=113，①
又第四行第二列的数为74+
| x-74 |
| 3 |
∴y+103=2（74+
| x-74 |
| 3 |
∴4x-3y=161②
由①②解得：x=50，y=13．
∴设第一列等差数列的首项为a1，公差为d，则d=0-y=-13，
∴0=a1+4d，
∴a1=52，即第一行第一列的数为52；
在第三列中，其公差d′=2x-103=100-103=-3，
∴第三列的首项为b1=b5-4d′=100-4×（-3）=112；
∵第一行中的数成等差数列，第一项a1=52，第三项为112，
∴第四项※=52+3×
| 112-52 |
| 2 |
故答案为：142．
点评：本题考查等差关系的确定，着重考查等差数列的通项公式，考查综合运算能力，属于中档题．
练习册系列答案
作业辅导系列答案
相关题目
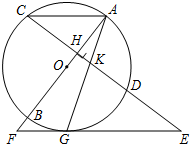如图，AB是⊙O的直径，弦CD⊥AB于H，过CD延长线上一点E作⊙O的切线交AB的延长线于F，切点为G，连接AG交CD于K，连接AC，且KG2=KD•GE．