题目内容
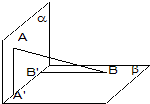如图，平面α⊥平面β，A∈α，B∈β，AB与两平面α、β所成的角分别为45°和30°，过A、B分别作两平面交线的垂线，垂足为A′、B′，则AB：A′B′=考点：点、线、面间的距离计算
专题：空间位置关系与距离
分析：连结AB′，设AB=2，则AA′=1，AB′=
，A′B′=
=1，由此能求出AB：A′B′．
| 2 |
| AB′2-AA′2 |
解答：
解：∵平面α⊥平面β，A∈α，B∈β，
AB与两平面α、β所成的角分别为45°和30°，
∴∠ABA'=30°，∠BAB'=45°，
连结AB′，设AB=2，则AA′=1，
∴AB′=
，
A′B′=
=1，
AB：A′B′=2：1．
故答案为：2：1．
AB与两平面α、β所成的角分别为45°和30°，
∴∠ABA'=30°，∠BAB'=45°，
连结AB′，设AB=2，则AA′=1，
∴AB′=
| 2 |
A′B′=
| AB′2-AA′2 |
AB：A′B′=2：1．
故答案为：2：1．
点评：本题考查两条线段的比值的求法，是中档题，解题时要注意空间思维能力的培养．
练习册系列答案
相关题目
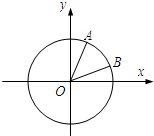如图，在平面直角坐标系xOy中，以Ox轴为始边作两个锐角α，β，它们的终边