题目内容
已知一个正四面体中,第一个球是它的内切球,第二个球是它的外接球,求这两个球的表面积之比及体积之比.
考点:球的体积和表面积
专题:计算题,空间位置关系与距离
分析:将正四面体ABCD,补成正方体,则正四面体ABCD的棱为正方体的面上对角线,根据正四面体ABCD外接球与内切球,画出图形,确定两个球的关系,通过正四面体的体积,求出两个球的半径的即可.
解答:
 解:将正四面体ABCD,补成正方体,则正四面体ABCD的棱为正方体的面上对角线,
解:将正四面体ABCD,补成正方体,则正四面体ABCD的棱为正方体的面上对角线,
设正四面体ABCD的棱长为a,则正方体的棱长为
a,
正四面体的外接球,就是以正四面体的棱为面对角线的正方体的外接球,
球的直径就是正方体的对角线的长,所以正方体的对角线为2R,
∵正方体的棱长为
a,所以
×
a=2R,
∴R=
a.
正四面体ABCD外接球与内切球的两球球心重合,设为O.
设DO的延长线与底面ABC的交点为E,则DE为正四面体的高,DE⊥底面ABC,
且DO=R,OE=r,OE=正四面体PABC内切球的半径.
设正四面体ABCD底面面积为S.
将球心O与四面体的4个顶点全部连接,
可以得到4个全等的正三棱锥,球心为顶点,以正四面体面为底面.
每个正三棱锥体积V1=
•S•r 而正四面体体积V2=
•S•(R+r)
从而有,4•V1=V2,
所以,4•
•S•r=
•S•(R+r),
所以,
=
.
∴这两个球的表面积之比为1:9,体积之比为1:27.
 解:将正四面体ABCD,补成正方体,则正四面体ABCD的棱为正方体的面上对角线,
解:将正四面体ABCD,补成正方体,则正四面体ABCD的棱为正方体的面上对角线,设正四面体ABCD的棱长为a,则正方体的棱长为
| ||
| 2 |
正四面体的外接球,就是以正四面体的棱为面对角线的正方体的外接球,
球的直径就是正方体的对角线的长,所以正方体的对角线为2R,
∵正方体的棱长为
| ||
| 2 |
| 3 |
| ||
| 2 |
∴R=
| ||
| 4 |
正四面体ABCD外接球与内切球的两球球心重合,设为O.
设DO的延长线与底面ABC的交点为E,则DE为正四面体的高,DE⊥底面ABC,
且DO=R,OE=r,OE=正四面体PABC内切球的半径.
设正四面体ABCD底面面积为S.
将球心O与四面体的4个顶点全部连接,
可以得到4个全等的正三棱锥,球心为顶点,以正四面体面为底面.
每个正三棱锥体积V1=
| 1 |
| 3 |
| 1 |
| 3 |
从而有,4•V1=V2,
所以,4•
| 1 |
| 3 |
| 1 |
| 3 |
所以,
| r |
| R |
| 1 |
| 3 |
∴这两个球的表面积之比为1:9,体积之比为1:27.
点评:本题考查球的表面积、体积公式,解题的关键是将正四面体ABCD,补成正方体,使得球O是正方体的外接球.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
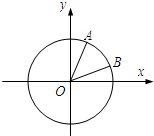 如图,在平面直角坐标系xOy中,以Ox轴为始边作两个锐角α,β,它们的终边
如图,在平面直角坐标系xOy中,以Ox轴为始边作两个锐角α,β,它们的终边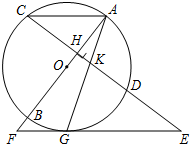 如图,AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于F,切点为G,连接AG交CD于K,连接AC,且KG2=KD•GE.
如图,AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于F,切点为G,连接AG交CD于K,连接AC,且KG2=KD•GE.