题目内容
已知圆C:(x-3)2+(y-4)2=4,直线l1:y=k(x-1),若l1与圆相交于P、Q两点,线段PQ的中点为M,A(1,0).
(1)求直线l1的斜率k的取值范围;
(2)求点M坐标(用k表示);
(3)已知l1与l2:x+2y+2=0的交点为N,问|AM|•|AN|是否为定值,若是,则求出定值;若不是,请说明理由.
(1)求直线l1的斜率k的取值范围;
(2)求点M坐标(用k表示);
(3)已知l1与l2:x+2y+2=0的交点为N,问|AM|•|AN|是否为定值,若是,则求出定值;若不是,请说明理由.
考点:直线和圆的方程的应用
专题:综合题,直线与圆
分析:(1)l1与圆相交于P、Q两点,可得
<2,即可求出直线l1的斜率k的取值范围;
(2)利用直线l1与圆C相交于P,Q两点,求线段PQ的中点M的坐标,直接转化为过圆心与直线l1垂直的中垂线方程,解两条直线方程的交点即可;
(3)分别联立相应方程,求得M,N的坐标,再求|AM|•|AN|.
| |2k-4| | ||
|
(2)利用直线l1与圆C相交于P,Q两点,求线段PQ的中点M的坐标,直接转化为过圆心与直线l1垂直的中垂线方程,解两条直线方程的交点即可;
(3)分别联立相应方程,求得M,N的坐标,再求|AM|•|AN|.
解答:
解:(1)∵l1与圆相交于P、Q两点,
∴
<2,
∴k>
;
(2)直线l1方程为y=k(x-1),
∵PQ⊥CM,∴CM方程为y-4=-
(x-3),即x+ky-3-4k=0.
与y=k(x-1),联立,可得M点坐标(
,
).
(3)由l1与l2:x+2y+2=0,联立得N(
,-
);
又M点坐标(
,
).
∴|AM|•|AN|=
•
•
=6为定值
∴
| |2k-4| | ||
|
∴k>
| 3 |
| 4 |
(2)直线l1方程为y=k(x-1),
∵PQ⊥CM,∴CM方程为y-4=-
| 1 |
| k |
与y=k(x-1),联立,可得M点坐标(
| k2+4k+3 |
| k2+1 |
| 4k2+2k |
| k2+1 |
(3)由l1与l2:x+2y+2=0,联立得N(
| 2k-2 |
| 2k+1 |
| 3k |
| 2k+1 |
又M点坐标(
| k2+4k+3 |
| k2+1 |
| 4k2+2k |
| k2+1 |
∴|AM|•|AN|=
| 2|2k+1| |
| 1+k2 |
| 1+k2 |
3
| ||
| |2k+1| |
点评:本题主要考查直线与圆的位置关系,圆的简单性质等基础知识.考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在平面直角坐标系xOy中,以Ox轴为始边作两个锐角α,β,它们的终边
如图,在平面直角坐标系xOy中,以Ox轴为始边作两个锐角α,β,它们的终边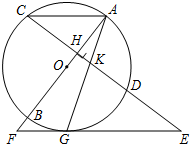 如图,AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于F,切点为G,连接AG交CD于K,连接AC,且KG2=KD•GE.
如图,AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于F,切点为G,连接AG交CD于K,连接AC,且KG2=KD•GE.