题目内容
已知平面中，若A（-4，0），B（4，0）且AC-BC=4，则动点C的轨迹方程是 ．
考点：轨迹方程,双曲线的定义
专题：计算题,圆锥曲线的定义、性质与方程
分析：根据A（-4，0），B（4，0）且AC-BC=4，可得动点C的轨迹是以A，B为焦点的双曲线的右支，a=2，c=4，即可求出动点C的轨迹方程．
解答：
解：∵A（-4，0），B（4，0）且AC-BC=4，
∴动点C的轨迹是以A，B为焦点的双曲线的右支，a=2，c=4，
∴b=
=2
，
∴动点C的轨迹方程是
-
=1（x＞0）．
故答案为：
-
=1（x＞0）．
∴动点C的轨迹是以A，B为焦点的双曲线的右支，a=2，c=4，
∴b=
| c2-a2 |
| 3 |
∴动点C的轨迹方程是
| x2 |
| 4 |
| y2 |
| 12 |
故答案为：
| x2 |
| 4 |
| y2 |
| 12 |
点评：本题考查双曲线的定义、动点轨迹方程的求法等知识，属于中档题．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
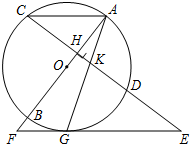如图，AB是⊙O的直径，弦CD⊥AB于H，过CD延长线上一点E作⊙O的切线交AB的延长线于F，切点为G，连接AG交CD于K，连接AC，且KG2=KD•GE．